간략한 요약
이 비디오는 내적의 개념을 선형 변환의 관점에서 설명합니다. 전통적인 내적 계산 방식과 기하학적 해석을 소개하고, 내적이 투영과 어떤 관련이 있는지, 그리고 선형 변환과의 관계를 통해 '이중성'이라는 수학적 개념을 설명합니다.
- 내적은 벡터의 투영과 관련이 있으며, 벡터가 같은 방향을 가리키는지 판단하는 데 유용합니다.
- 선형 변환은 1x2 행렬로 표현될 수 있으며, 이는 벡터의 내적과 계산적으로 동일합니다.
- '이중성'은 벡터와 선형 변환 사이의 자연스럽고 놀라운 대응 관계를 나타냅니다.
내적 소개 및 기하학적 해석 [0:20]
내적은 일반적으로 선형대수 강의 초반에 소개되지만, 이 비디오에서는 선형 변환에 대한 이해를 돕기 위해 뒤쪽에 배치되었습니다. 내적은 같은 차원의 두 벡터에서 같은 위치의 좌표값을 곱한 후 모두 더하는 방식으로 계산됩니다. 기하학적으로는 한 벡터를 다른 벡터에 투영한 후 투영된 벡터의 길이에 원래 벡터의 길이를 곱한 값으로 해석할 수 있습니다. 투영 방향에 따라 내적은 양수, 음수 또는 0이 될 수 있습니다.
내적의 대칭성과 스케일링 [2:10]
내적은 순서에 상관없이 결과가 동일하다는 대칭성을 가집니다. 이는 한 벡터를 다른 벡터에 투영하는 방식이 서로 대칭적이기 때문입니다. 벡터 중 하나를 스케일링하면 내적 값도 그 비율만큼 변합니다. 스케일링은 투영되는 벡터의 길이 또는 투영을 받는 벡터의 길이에 영향을 미치므로, 어느 쪽으로 투영하든 내적 값은 동일하게 스케일링됩니다.
선형 변환과 1차원 변환 [3:57]
좌표값을 곱하고 더하는 계산과 투영 사이의 관계를 이해하려면 선형 변환의 개념을 알아야 합니다. 특히, 다차원에서 1차원 수선으로의 선형 변환에 주목합니다. 이러한 변환은 2차원 벡터를 입력받아 숫자 하나를 출력하는 함수로 볼 수 있습니다. 선형 변환은 입력 공간에서 같은 간격의 점들이 출력 공간에서도 같은 간격을 유지하는 특징을 가집니다.
행렬-벡터 곱셈과 내적의 연결 [5:41]
선형 변환은 기저 벡터(i-hat, j-hat)의 도착 위치에 의해 완전히 결정됩니다. 2차원에서 1차원으로의 선형 변환은 1x2 행렬로 표현될 수 있으며, 이 행렬을 벡터에 적용하는 것은 행렬-벡터 곱셈과 같습니다. 이러한 계산은 두 벡터의 내적과 동일하게 느껴질 수 있습니다. 1x2 행렬과 2차원 벡터 사이에는 밀접한 관련성이 있으며, 이는 기하학적 관점에서 중요한 의미를 가집니다.
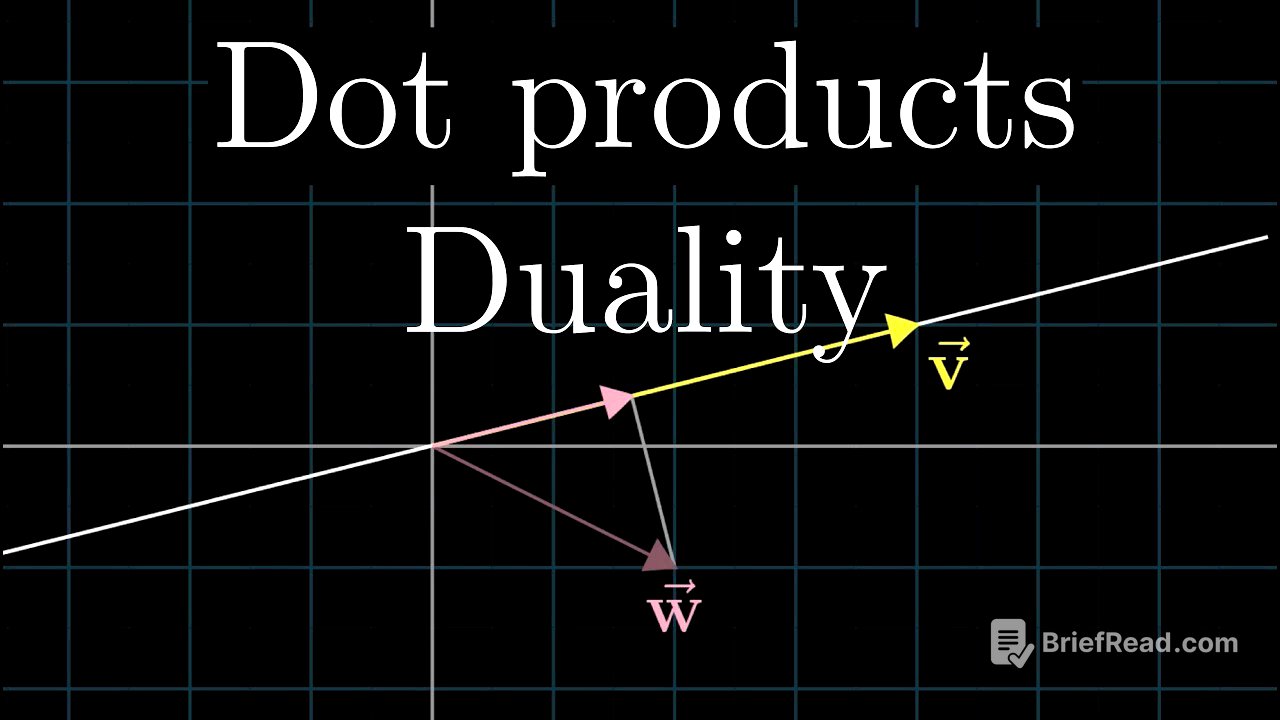
투영과 선형 변환의 관계 [7:15]
2차원 벡터를 대각선 방향의 수선에 투영하는 것은 2차원 벡터를 입력받아 숫자를 출력하는 선형 함수를 정의하는 것과 같습니다. 이 함수는 선형적이며, 1x2 행렬로 나타낼 수 있습니다. 투영 변환을 나타내는 1x2 행렬은 수선의 단위 벡터(u-hat)의 좌표와 같습니다. 따라서 임의의 벡터를 투영하는 것은 해당 행렬에 벡터를 곱하는 것과 같으며, 이는 u-hat과의 내적과 계산적으로 동일합니다.
일반화된 내적과 이중성 [10:34]
단위 벡터가 아닌 일반적인 벡터의 경우에도 동일한 원리가 적용됩니다. 벡터를 스케일링하면 해당 벡터와 관련된 행렬도 스케일링됩니다. 이는 벡터 위로 투영한 후 벡터의 길이만큼 투사체 길이를 늘리는 것으로 해석할 수 있습니다. 이러한 선형 변환은 1x2 행렬로 표현될 수 있으며, 이는 2차원 벡터와의 내적과 같습니다. 따라서 선형 변환은 항상 특정 벡터와 관련되어 있으며, 변환의 적용은 벡터의 내적을 구하는 것과 같습니다. 이러한 관계를 통해 '이중성'이라는 수학적 개념을 이해할 수 있습니다. 벡터의 '이중'은 해당 벡터가 가진 선형 변환의 성질을 나타내며, 1차원으로 변환시키는 선형 변환에서 '이중'은 공간상의 특정 벡터를 의미합니다.