TEOREMA DE CASTIGLIANO EN VIGAS EJERCICIOS RESUELTOS PASO A PASO Y FÁCIL

Resumen Breve

Este video demuestra cómo calcular el desplazamiento vertical en un punto específico de una viga utilizando el teorema de Castigliano. Los puntos clave incluyen la aplicación de una carga ficticia, el cálculo de reacciones, la generación de ecuaciones de momento, la aplicación de derivadas parciales y la sustitución en la fórmula del teorema de Castigliano. Finalmente, se verifica el resultado con un software de análisis estructural (Ftool).

• Aplicación del teorema de Castigliano para calcular el desplazamiento vertical.
• Uso de una carga ficticia para facilitar el cálculo.
• Verificación del resultado mediante software de análisis estructural.

Introducción al Problema

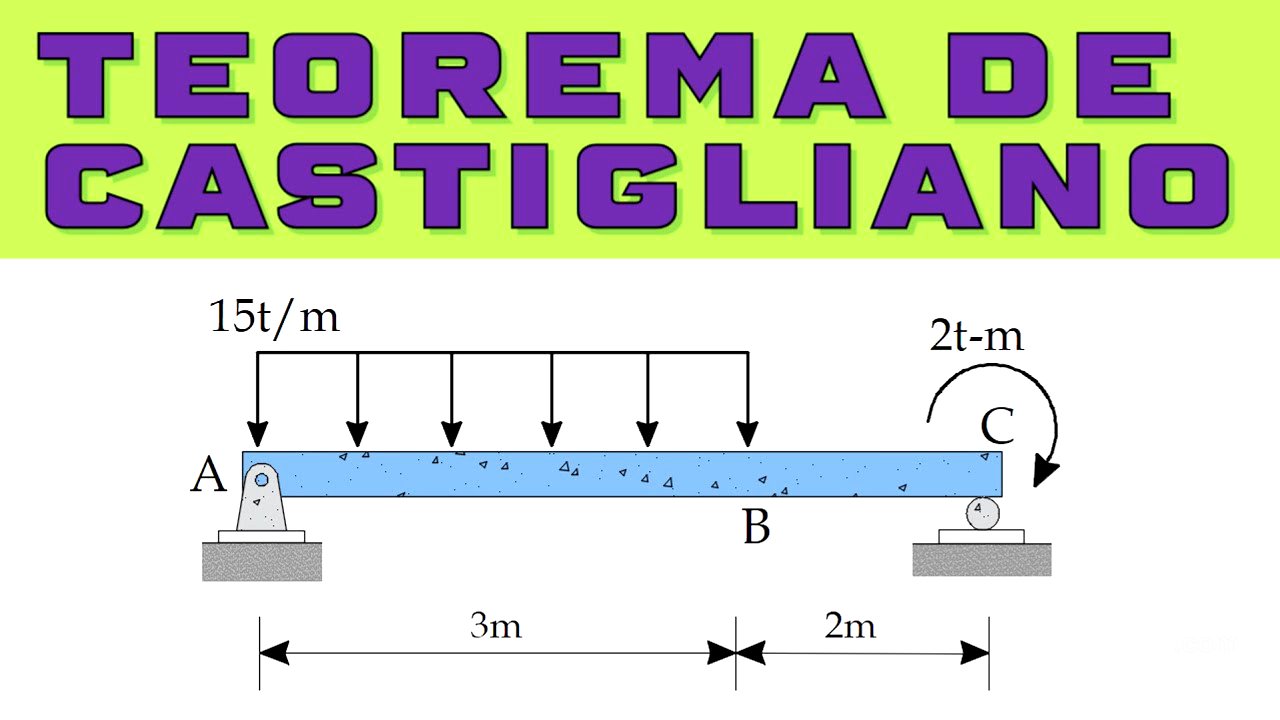
Se presenta un ejercicio para calcular el desplazamiento vertical del punto B en una viga utilizando el teorema de Castigliano. Se identifica la estructura como isostática debido a la presencia de un apoyo fijo y un apoyo móvil, sin cargas complejas adicionales.

Paso 1: Aplicación de la Carga Ficticia

Se aplica una carga ficticia 'p' en el punto B, donde se busca calcular el desplazamiento vertical. Esta carga se asume verticalmente hacia abajo. Se calculan las reacciones en los apoyos (Ay y Cy) en función de esta carga ficticia 'p'. Primero, se determina la fuerza resultante de la carga rectangular (45 toneladas) y su ubicación (1.5 m desde el punto A). Luego, se aplican las ecuaciones de equilibrio estático (sumatoria de momentos y fuerzas verticales) para encontrar las reacciones Ay y Cy en términos de 'p'. Los resultados son: Cy = 13.5 + 0.6p y Ay = 31.5 + 0.4p.

Paso 2: Generación de Ecuaciones de Momento

Se generan las ecuaciones de momento aplicando cortes en los tramos de la viga. Se identifican dos tramos: de A a B y de C a B. Para el primer tramo (corte 1), que va de A a B (0 a 3 metros), se realiza un corte de izquierda a derecha, obteniendo la ecuación de momento M1 = 31.10x + 0.4px - 7.5x². Se calcula la derivada parcial de M1 con respecto a p, resultando en ∂M1/∂p = 0.4x. Para el segundo tramo (corte 2), que va de C a B (0 a 2 metros), se realiza un corte de derecha a izquierda, obteniendo la ecuación de momento M2 = 13.90x + 0.6px - 2. La derivada parcial de M2 con respecto a p es ∂M2/∂p = 0.6x.

Paso 3: Aplicación de la Fórmula de Castigliano

Se aplica la fórmula del teorema de Castigliano para calcular el desplazamiento vertical en el punto B. Se establece que la variable p se asume como cero en las ecuaciones de momento originales, ya que su propósito principal era facilitar el cálculo de las derivadas parciales. Se reemplazan las ecuaciones de momento (con p=0) y sus derivadas parciales en la fórmula de Castigliano, integrando sobre los tramos correspondientes. La fórmula general es: Desplazamiento = ∫(M * ∂M/∂p) dx / (E*I).

Cálculo del Desplazamiento Vertical

Se calcula el desplazamiento vertical del punto B integrando las ecuaciones de momento y sus derivadas parciales sobre los tramos correspondientes. Para el corte 1 (0 a 3 metros), la integral resulta en 51.21 toneladas por metros al cubo. Para el corte 2 (0 a 2 metros), la integral resulta en 19.84 toneladas por metros al cubo. La suma de estas integrales da un desplazamiento total de 71.05 toneladas por metros al cubo, dividido por EI (módulo de elasticidad por inercia).

Interpretación del Resultado y Comprobación

El resultado positivo indica que la deformación ocurre en la dirección asumida (hacia abajo). Se realiza una comprobación utilizando el software Ftool, donde se modela la viga con las cargas y condiciones de apoyo especificadas. El resultado obtenido en Ftool coincide con el cálculo manual, validando el proceso y el resultado obtenido mediante el teorema de Castigliano.