Resumen Breve
Este video demuestra cómo calcular el desplazamiento vertical en un punto específico de una viga utilizando el método de Castigliano. Los pasos clave incluyen aplicar una carga ficticia en el punto de interés, calcular las reacciones en función de esta carga, determinar las ecuaciones de momento mediante cortes, aplicar la fórmula de Castigliano y, finalmente, evaluar la integral para obtener el desplazamiento.
- Aplicación de carga ficticia en el punto donde se desea calcular el desplazamiento.
- Cálculo de reacciones en función de la carga ficticia.
- Determinación de ecuaciones de momento mediante cortes en la viga.
- Aplicación de la fórmula de Castigliano para hallar el desplazamiento vertical.
Introducción al Problema y Carga Ficticia
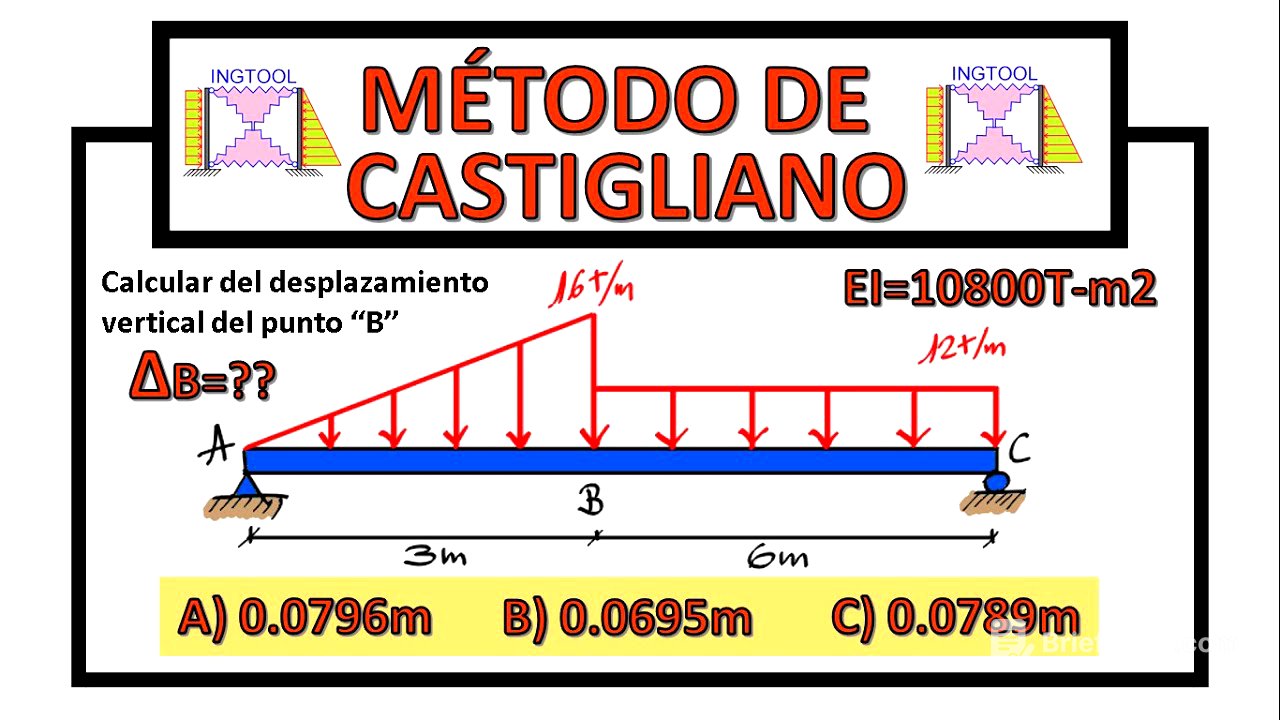
Se presenta un problema donde se debe calcular el desplazamiento vertical en el punto B de una viga utilizando el método de Castigliano. Se explica que el primer paso es aplicar una carga ficticia en el punto donde se quiere calcular el desplazamiento. Si se busca un desplazamiento vertical, se aplica una fuerza vertical; si se busca un giro, se aplica un momento. En este caso, se coloca una carga vertical "p" en el punto B.
Cálculo de Reacciones
Una vez colocada la carga ficticia, se calculan las reacciones en los apoyos de la viga en función de esta carga "p". Se identifican las reacciones verticales en los apoyos A y C (Ay y Cy). Se aplican las ecuaciones de equilibrio estático (sumatoria de momentos en A y sumatoria de fuerzas en y) para resolver las reacciones Ay y Cy en términos de la carga distribuida y la carga ficticia "p". Se obtienen los valores de Cy y Ay en función de "p".
Ecuaciones de Momento: Corte 1 (A a B)
Se establecen las ecuaciones de momento para la viga mediante cortes. Se realiza un corte de izquierda a derecha entre los puntos A y B (corte 1), en el intervalo de 0 a 3 metros. Se dibuja el diagrama de cuerpo libre del segmento cortado, incluyendo la reacción Ay y la carga triangular distribuida. Se calcula la altura de la carga triangular en función de la distancia "x" y se determina la fuerza resultante de la carga triangular. Se plantea la ecuación de momento (M1) en función de "x" y de la reacción Ay. Se simplifica la ecuación del momento.
Ecuaciones de Momento: Corte 2 (C a B)
Se realiza un segundo corte de derecha a izquierda entre los puntos C y B (corte 2), en el intervalo de 0 a 6 metros. Se dibuja el diagrama de cuerpo libre del segmento cortado, incluyendo la reacción Cy y la carga rectangular distribuida. Se calcula la fuerza resultante de la carga rectangular y se plantea la ecuación de momento (M2) en función de "x" y de la reacción Cy.
Aplicación de la Fórmula de Castigliano
Se aplica la fórmula de Castigliano para calcular el desplazamiento vertical en B. Se establece que el desplazamiento vertical en B es igual a la integral del producto de la ecuación de momento por la derivada parcial de esa ecuación de momento con respecto a la carga "p", dividido por el producto del módulo de elasticidad (E) y la inercia (I). Se indica que el valor de la carga ficticia "p" se hace igual a cero después de haber calculado las derivadas parciales.
Resolución de Integrales y Cálculo del Desplazamiento
Se reemplazan las ecuaciones de momento y sus derivadas parciales en la fórmula de Castigliano. Se evalúan las integrales para los cortes 1 y 2, utilizando los límites de integración correspondientes. Se realiza el cálculo numérico y se obtiene el valor del desplazamiento vertical en B antes de dividir por EI. Se reemplaza el valor de EI y se realiza la división para obtener el desplazamiento vertical final en metros. Se analiza el signo del resultado para determinar la dirección del desplazamiento.
![💥¿Qué es Química Orgánica y Química Inorgánica?💧 [Fácil y Rápido] | QUÍMICA |](https://wm-img.halpindev.com/p-briefread_c-10_b-10/urlb/aHR0cDovL2ltZy55b3V0dWJlLmNvbS92aS9OMEd3R0pGcFlSTS9ocWRlZmF1bHQuanBn.jpg)
