Breve Resumen
Este video explica cómo resolver sistemas de ecuaciones 2x2 utilizando el método gráfico. Daniel Carreón repasa los conceptos básicos de los sistemas de ecuaciones, explica el método gráfico y luego resuelve un ejercicio paso a paso, incluyendo la comprobación de los resultados. Finalmente, propone ejercicios de práctica.
- Repaso de conceptos básicos de ecuaciones 2x2.
- Explicación del método gráfico para resolver sistemas de ecuaciones.
- Resolución de un ejercicio práctico y comprobación de los resultados.
Bienvenida [0:00]
Daniel Carreón da la bienvenida al video y anuncia que explicará cómo resolver sistemas de ecuaciones 2x2 mediante el método gráfico.
Conceptos básicos [0:25]
Un sistema de ecuaciones 2x2 es un conjunto de dos ecuaciones que comparten dos incógnitas. Resolver un sistema de ecuaciones implica encontrar los valores de las incógnitas, generalmente representadas como 'x' e 'y'. El método gráfico consiste en representar las gráficas asociadas a las ecuaciones del sistema, donde la solución es el punto de intersección de estas gráficas.
Ejercicio [1:04]
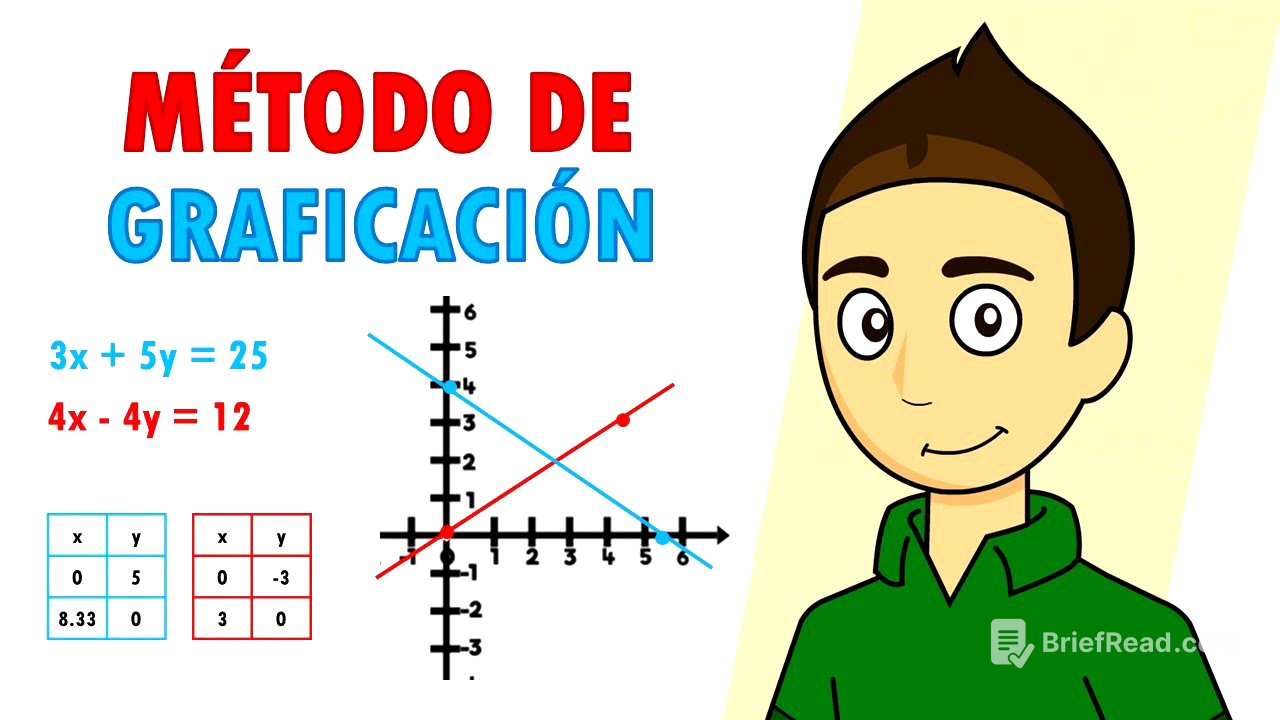
Daniel presenta el sistema de ecuaciones: 3x + 5y = 25 y 4x - 4y = 12. Para resolverlo gráficamente, crea tablas para encontrar dos coordenadas por cada ecuación. Primero, sustituye x = 0 en la primera ecuación para encontrar el valor de y, obteniendo y = 5. Luego, sustituye y = 0 para encontrar x = 8.33. Repite el proceso con la segunda ecuación, sustituyendo x = 0 para obtener y = -3, y luego y = 0 para obtener x = 3.
Ejercicios de repaso [6:48]
Una vez obtenidas las coordenadas, Daniel las grafica en el plano cartesiano. Traza una línea recta que pasa por los dos puntos de cada ecuación. El punto de intersección de estas dos rectas indica los valores de x e y que resuelven el sistema de ecuaciones. En este caso, el punto de intersección es x = 5 e y = 2. Para comprobar los resultados, sustituye estos valores en ambas ecuaciones originales. Si ambos lados de las ecuaciones son iguales después de la sustitución, los resultados son correctos. Finalmente, Daniel propone ejercicios para que los espectadores practiquen.