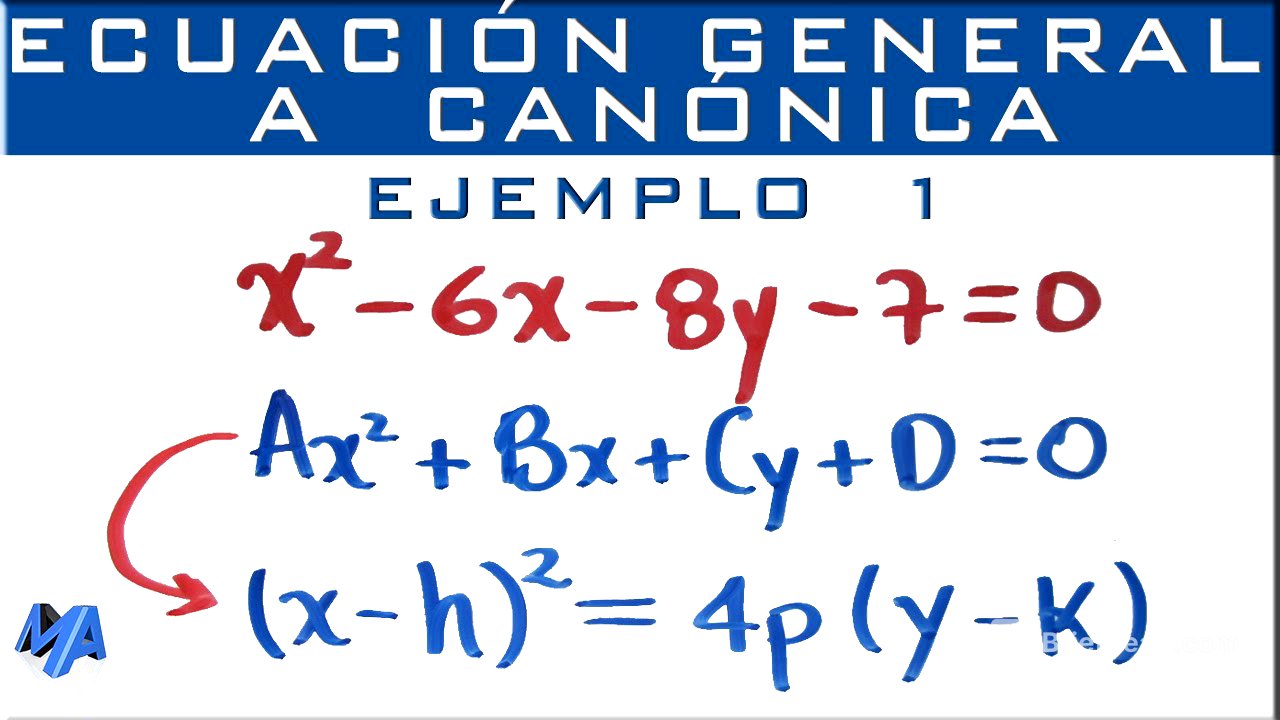Breve Resumen
Este video explica cómo convertir una ecuación general de una parábola a su forma canónica. El proceso implica aislar los términos con 'x' en un lado de la ecuación, completar el trinomio cuadrado perfecto, factorizar y simplificar para obtener la forma canónica. Se proporciona un ejemplo detallado y un ejercicio de práctica para reforzar la comprensión.
- Aislar términos con 'x' y completar el trinomio cuadrado perfecto.
- Factorizar para simplificar la ecuación.
- Aplicar los mismos pasos para resolver ejercicios similares.
Conceptos Clave [0:15]
Para transformar la ecuación general de una parábola a su forma canónica, se deben agrupar los términos que contienen la variable 'x' en un lado de la ecuación y los términos restantes en el otro lado. Es crucial recordar que al pasar términos de un lado a otro de la igualdad, sus signos cambian. El objetivo es manipular la ecuación para que coincida con la forma canónica, lo cual facilita la identificación de elementos clave de la parábola como el vértice y el foco.
Solución del Ejemplo [0:58]
Se detalla el proceso para convertir una ecuación general a su forma canónica. Primero, se agrupan los términos con 'x' a la izquierda y los demás a la derecha, cambiando los signos al moverlos. Luego, se completa el trinomio cuadrado perfecto sumando un término calculado a partir del coeficiente de 'x' (la mitad de este coeficiente, elevada al cuadrado) a ambos lados de la ecuación. Este trinomio se factoriza como un binomio al cuadrado. Finalmente, se factoriza el lado derecho para aislar 'y', obteniendo la forma canónica.
Ejercicio de Práctica [5:40]
Se presenta un ejercicio para practicar la conversión de una ecuación general a la forma canónica. Se dan los pasos para resolverlo: se agrupan los términos con 'x' a un lado, se completa el trinomio cuadrado perfecto, se factoriza y se simplifica la ecuación. La solución muestra cómo aplicar los mismos principios para resolver problemas similares, reforzando la comprensión del proceso.