Resumen Breve
Este video explica cómo calcular el desplazamiento vertical y la rotación en un punto específico de una viga en voladizo utilizando el teorema de Castigliano. Se introduce el concepto de carga ficticia y cómo aplicarla para determinar las ecuaciones de momento necesarias. El video detalla el proceso paso a paso, desde la aplicación de la carga ficticia hasta la resolución de la integral para obtener los resultados finales, los cuales son verificados con un software de análisis estructural.
- Se aplica una carga ficticia para calcular el desplazamiento vertical y el giro en un punto específico de la viga.
- Se utilizan las ecuaciones de momento y derivadas parciales para aplicar el teorema de Castigliano.
- Los resultados se verifican con un software de análisis estructural para confirmar su validez.
Introducción al Problema y el Teorema de Castigliano [0:00]
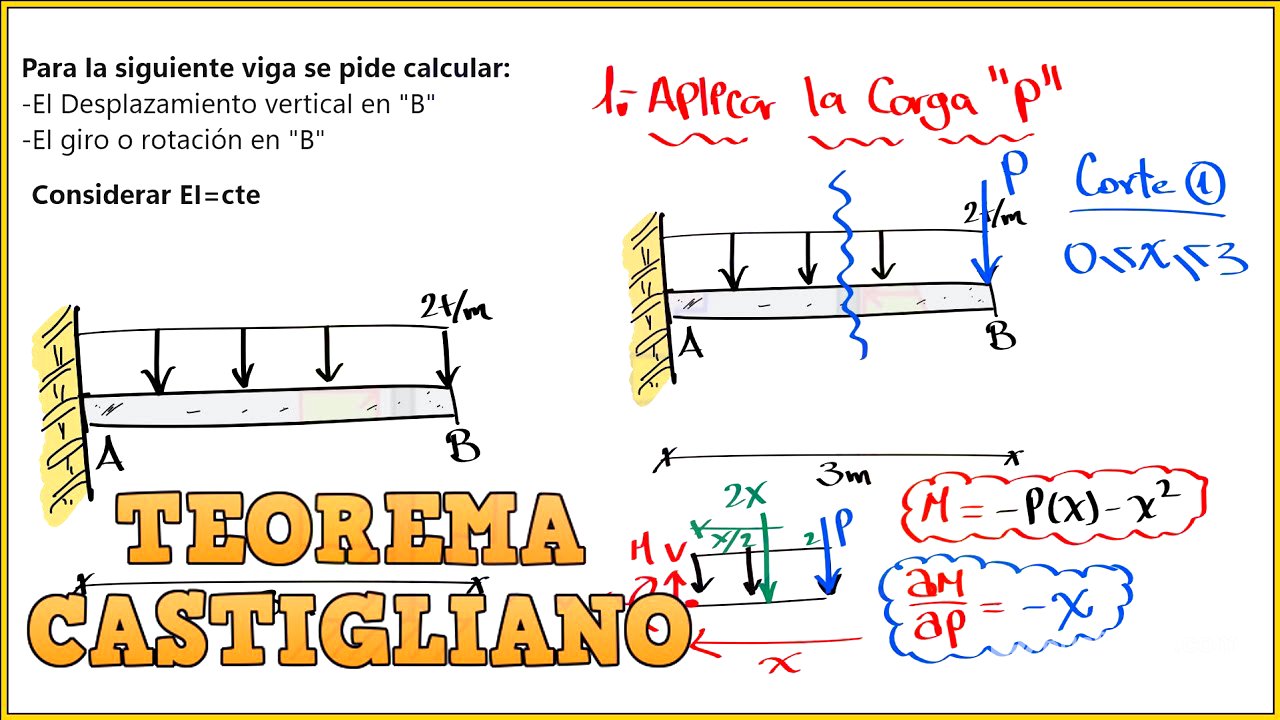
Se presenta el problema de calcular el desplazamiento vertical y la rotación en el punto B de una viga en voladizo con un EI constante, sometida a una carga distribuida rectangular. Se introduce el teorema de Castigliano como el método para calcular las deformaciones en la estructura. El primer paso consiste en aplicar una carga ficticia en el punto donde se desea calcular la deformación.
Aplicación de la Carga Ficticia para el Desplazamiento Vertical [0:44]
Para calcular el desplazamiento vertical en el punto B, se aplica una carga ficticia (P) en ese punto. Se realiza un corte en la viga y se determina la ecuación de momento utilizando el método de derecha a izquierda, lo cual simplifica el cálculo al no requerir el cálculo previo de las reacciones en el empotramiento. Se calcula la derivada parcial de la ecuación de momento con respecto a la carga ficticia P.
Cálculo del Desplazamiento Vertical Usando la Fórmula de Castigliano [5:38]
Se aplica la fórmula del teorema de Castigliano, que involucra la integral del producto de la ecuación de momento y su derivada parcial con respecto a la carga ficticia, dividida por EI. Se recuerda que la carga ficticia P se iguala a cero en la ecuación de momento antes de realizar la integral. Se resuelve la integral (manualmente o con calculadora) para obtener el valor del desplazamiento vertical en el punto B. Se analizan las unidades del resultado para asegurar la coherencia física.
Verificación del Desplazamiento Vertical con Software [9:13]
Se utiliza el software Ftool para verificar el resultado del desplazamiento vertical calculado manualmente. Se explica la diferencia de signo entre el resultado manual (positivo) y el del software (negativo) debido a la convención de signos utilizada por el programa, confirmando la validez del cálculo manual.
Aplicación de la Carga de Momento Ficticio para el Cálculo del Giro [10:18]
Para calcular el giro en el punto B, se reemplaza la carga vertical ficticia por un momento ficticio (M). Se ajusta la ecuación de momento para reflejar la presencia del momento ficticio. Se calcula la derivada parcial de la ecuación de momento con respecto al momento ficticio M.
Cálculo del Giro Usando la Fórmula de Castigliano [12:35]
Se aplica nuevamente la fórmula del teorema de Castigliano, utilizando la ecuación de momento con el momento ficticio y su derivada parcial. Se resuelve la integral para obtener el valor del giro en el punto B. Se analizan las unidades del resultado para asegurar la coherencia física.
Verificación del Giro con Software [14:11]
Se utiliza el software Ftool para verificar el resultado del giro calculado manualmente. Se explica la diferencia de signo entre el resultado manual (positivo) y el del software (negativo) debido a la convención de signos utilizada por el programa, confirmando la validez del cálculo manual. Se concluye que el giro es horario, lo cual coincide con la dirección del momento ficticio aplicado.
Conclusión y Próximos Pasos [14:59]
Se resume el proceso de cálculo del desplazamiento vertical y el giro en una viga utilizando el teorema de Castigliano. Se menciona la posibilidad de aplicar el segundo teorema de Castigliano para estructuras hiperestáticas y la aplicabilidad del método a diferentes tipos de estructuras, como pórticos y armaduras. Se invita a los espectadores a compartir el video y dejar comentarios para futuros contenidos.