Distribuciones de probabilidad: binomial, Poisson y normal

Breve Resumen

Este video explica los conceptos básicos de probabilidad y cómo se aplican en las distribuciones de probabilidad, tanto discretas como continuas. Se centra en la distribución binomial, de Poisson y normal, mostrando cómo calcular probabilidades en Excel y cómo interpretar los resultados.

• Probabilidad básica y espacio muestral.
• Distribuciones binomial, Poisson y normal.
• Uso de Excel para cálculos de probabilidad.

Introducción a la Probabilidad

La probabilidad es un valor entre 0 y 1 que indica la posibilidad de que ocurra un evento. Un evento imposible tiene probabilidad 0, mientras que un evento seguro tiene probabilidad 1. El experimento es el proceso que lleva a un resultado o evento. El espacio muestral es el conjunto de todos los posibles resultados de un experimento. La probabilidad clásica se aplica cuando cada evento tiene la misma probabilidad de ocurrir. Por ejemplo, al lanzar un dado, la probabilidad de que caiga cualquier número es 1/6.

Probabilidad Clásica y Ejemplos

La probabilidad clásica permite calcular probabilidades exactas al conocer el número total de posibles resultados y el número de resultados favorables. Por ejemplo, la probabilidad de obtener un número par al lanzar un dado se calcula dividiendo el número de resultados favorables (3) entre el número total de resultados posibles (6), resultando en 0.5. Para problemas más complejos, como la probabilidad de obtener al menos una cara al lanzar dos veces una moneda, es necesario definir el espacio muestral completo y contar los eventos favorables.

Distribución de Probabilidad y Distribución Binomial

Una distribución de probabilidad muestra todos los posibles resultados de un experimento junto con sus probabilidades. La distribución binomial se aplica cuando hay solo dos resultados posibles: éxito y fracaso. Se presenta un ejemplo de un lote de celulares donde el 20% están defectuosos y se toman muestras de cinco en cinco. Se explica que, aunque lo más probable es encontrar un celular defectuoso por muestra, también existe la posibilidad de no encontrar ninguno o de que todos estén defectuosos, aunque esta última es menos probable.

Cálculo de Probabilidad Binomial en Excel

Se muestra cómo utilizar Excel para calcular probabilidades binomiales. Se utiliza la función "DISTR.BINOM.N" para calcular la probabilidad de obtener un número específico de éxitos en un número dado de ensayos. Se explica cómo fijar las celdas de la probabilidad de éxito y el tamaño de la muestra para poder arrastrar la fórmula y obtener los resultados para diferentes números de éxitos. Se verifica que la suma de todas las probabilidades del espacio muestral sea igual a 1.

Distribución de Poisson y su Aplicación

La distribución de Poisson describe el número de veces que se presenta un evento durante un intervalo específico, generalmente de tiempo. Se presenta un ejemplo de un banco donde llegan en promedio 7.8 personas por hora. Se plantea la pregunta de cuál es la probabilidad de que lleguen más de 10 personas en la siguiente hora. Se explica cómo resolver este problema utilizando Excel.

Cálculo de Probabilidad de Poisson en Excel

Se demuestra cómo usar Excel para calcular probabilidades de Poisson. Se utiliza la función "DISTR.POISSON" para calcular la probabilidad de que ocurra un número específico de eventos en un intervalo dado. Se explica cómo usar la función de distribución acumulada para calcular la probabilidad de que ocurran hasta un cierto número de eventos y cómo restar este valor de 1 para obtener la probabilidad de que ocurran más de ese número de eventos.

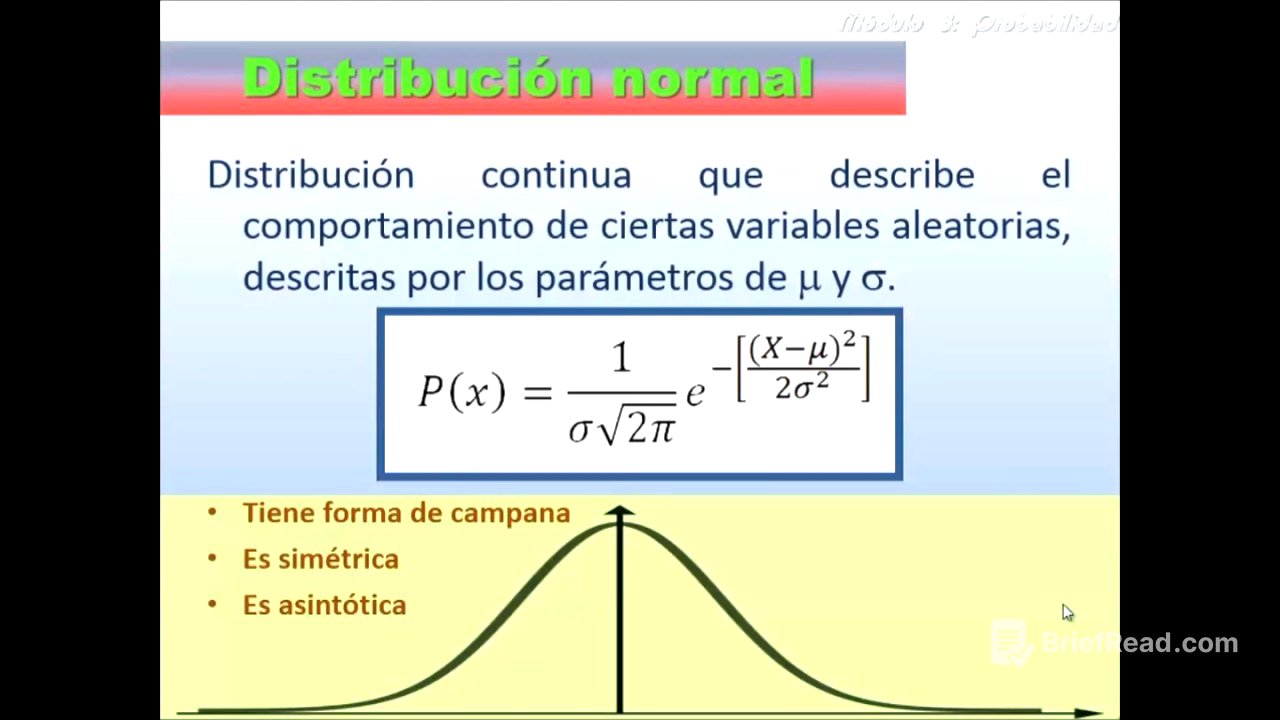
Distribución Normal y sus Características

La distribución normal se define por la media y la desviación estándar. Se explica que muchas variables tienen un comportamiento normal, donde la mayoría de los datos se agrupan alrededor de la media y hay pocos datos en los extremos. Se muestra cómo la distribución se aproxima a una curva de campana simétrica a medida que aumenta el tamaño de la muestra. Se mencionan las características de la distribución normal, como que el 68.3% de la población se encuentra entre una desviación estándar de la media, el 95.5% entre dos desviaciones estándar y el 99.7% entre tres desviaciones estándar.

Aplicación de la Distribución Normal y Cálculo en Excel

Se presenta un problema donde el peso medio de una población es de 157 libras con una desviación estándar de 34 libras, y se quiere saber qué proporción de la población pesa entre 140 y 170 libras. Se explica cómo calcular esta proporción utilizando Excel y la función "DISTR.NORM.N". Se muestra cómo calcular el área bajo la curva hasta 140 y hasta 170, y cómo restar estos valores para obtener el área entre 140 y 170, que representa la proporción de la población que pesa entre esos valores.

Otras Distribuciones de Probabilidad

Se mencionan otras distribuciones de probabilidad importantes, como la exponencial, hipergeométrica, t de Student, chi cuadrada y distribución F, que son ampliamente utilizadas en estadística inferencial para describir estados particulares de la naturaleza. Se concluye que las distribuciones de probabilidad son herramientas esenciales en estadística.