Resumen Breve
Este video explica cómo calcular la distancia entre dos puntos utilizando el método gráfico. Se basa en la formación de triángulos rectángulos y la aplicación del teorema de Pitágoras para encontrar la longitud de la hipotenusa, que representa la distancia entre los puntos. Incluye ejemplos prácticos y un ejercicio para practicar.
- Se utiliza el teorema de Pitágoras para calcular la distancia.
- Se explica cómo formar triángulos rectángulos utilizando los puntos dados.
- Se proporcionan ejemplos prácticos para comprender el concepto.
Saludo [0:00]
El video comienza con un saludo y una introducción al tema del curso sobre la ecuación de la recta, específicamente cómo encontrar la distancia entre dos puntos utilizando el método gráfico.
Conceptos que debes saber [0:22]
El video explica que para encontrar la distancia entre dos puntos en un plano cartesiano, se debe trazar una recta entre los dos puntos y luego formar un triángulo rectángulo donde esta recta sea la hipotenusa. Se pueden formar dos triángulos rectángulos diferentes, pero ambos serán semejantes y tendrán las mismas medidas en sus catetos.
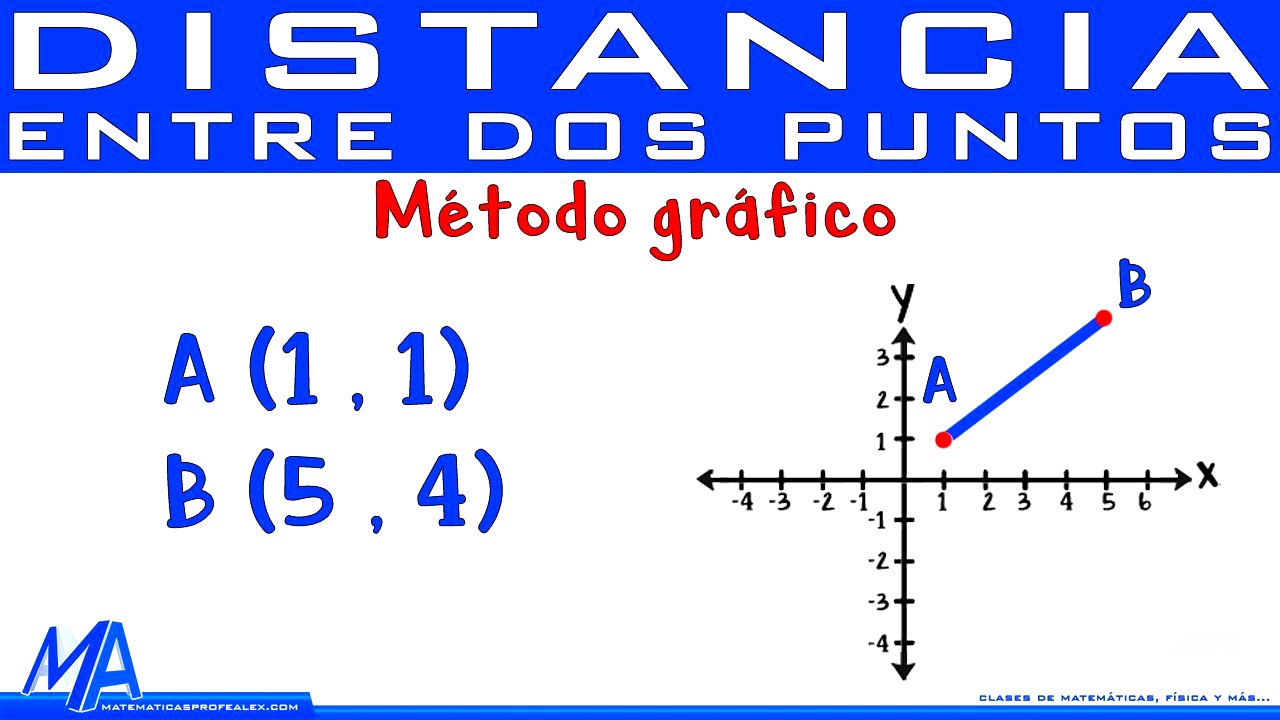
Solución del ejemplo [0:29]
Se explica cómo encontrar la distancia entre los puntos A(1,1) y B(5,4). Se forma un triángulo rectángulo con la recta que une los puntos A y B como hipotenusa. Los catetos del triángulo miden 3 y 4 unidades respectivamente. Aplicando el teorema de Pitágoras (distancia² = 3² + 4²), se calcula la distancia como la raíz cuadrada de 25, que es 5 unidades.
Solución del ejemplo 2 [6:40]
Se explica cómo encontrar la distancia entre los puntos C(3,-2) y D(-3,5). Se forma un triángulo rectángulo con la recta que une los puntos C y D como hipotenusa. Los catetos del triángulo miden 7 y 6 unidades respectivamente. Aplicando el teorema de Pitágoras (distancia² = 7² + 6²), se calcula la distancia como la raíz cuadrada de 85, que es aproximadamente 9.2 unidades.
Ejercicio de práctica [10:29]
Se proponen tres ejercicios para practicar el cálculo de la distancia entre puntos: A y B, C y D, y E y F. Se proporcionan las respuestas: la distancia entre A y B es 10, entre C y D es la raíz cuadrada de 29 (aproximadamente 5.38), y entre E y F es 5 (este último sin necesidad de formar un triángulo por ser una línea vertical).


![AGENDA Alpha Draconiana y FALSA 2da VENIDA de "CRISTO" Holograma- Blue BEAM/ Alex COLLIER [Dob ESP]](https://wm-img.halpindev.com/p-briefread_c-10_b-10/urlb/aHR0cDovL2ltZy55b3V0dWJlLmNvbS92aS9qTEkzdWE3dkhPSS9ocWRlZmF1bHQuanBn.jpg)





