Resumen Breve
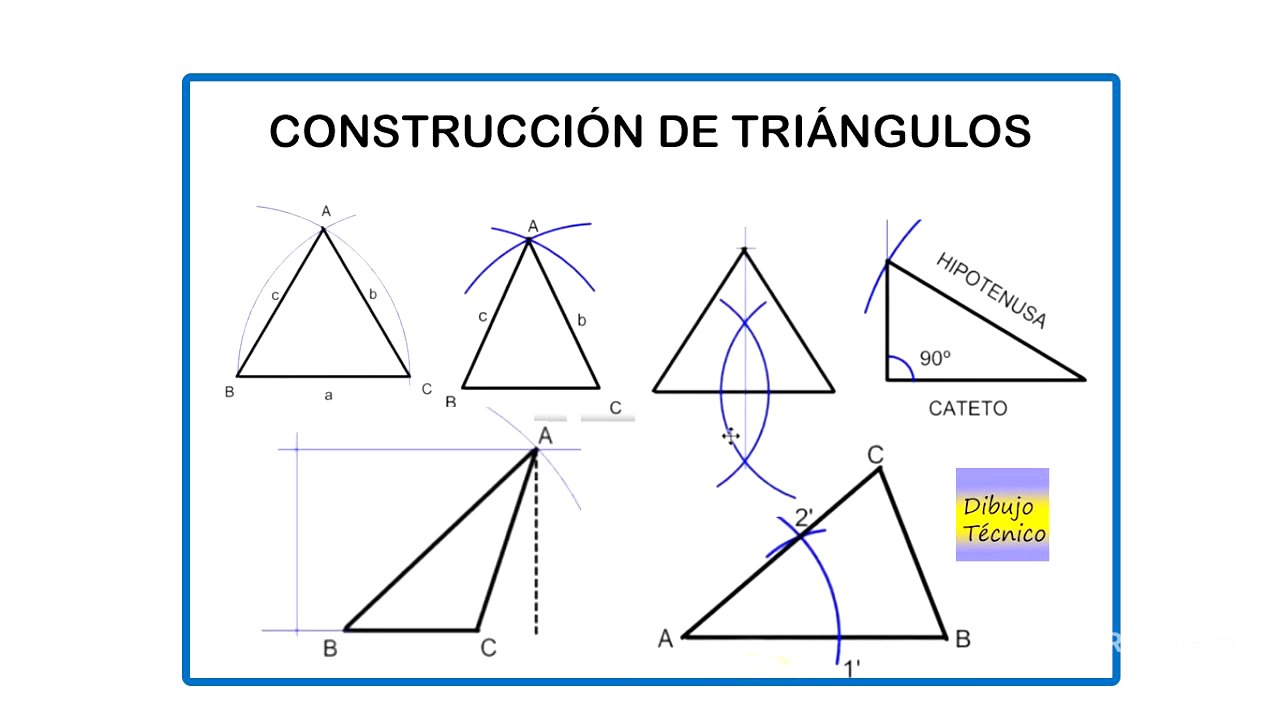
Este video tutorial demuestra paso a paso cómo construir diferentes tipos de triángulos utilizando regla y compás. Se explica la construcción de triángulos equiláteros, isósceles (conociendo los lados y conociendo la base y su altura), rectángulos (conociendo su hipotenusa y un cateto) y escalenos (conociendo la altura y dos lados). Además, se muestra cómo dibujar un triángulo cuando se conocen las longitudes de dos lados y el ángulo entre ellos.
- Construcción de triángulos equiláteros, isósceles, rectángulos y escalenos.
- Uso de regla y compás para mediciones precisas.
- Aplicación de conceptos geométricos como mediatriz y ángulos rectos.
Construcción de un Triángulo Equilátero [0:06]
Para construir un triángulo equilátero, se comienza dibujando un lado de 6 centímetros como base. Luego, con un compás ajustado a la misma medida de 6 centímetros, se trazan arcos desde cada extremo de la base. El punto donde se intersecan los arcos determina el tercer vértice del triángulo. Finalmente, se unen los extremos de la base con este vértice para completar el triángulo equilátero, asegurando que los tres lados sean iguales.
Construcción de un Triángulo Isósceles (Conociendo los Lados) [1:35]
Para construir un triángulo isósceles con dos lados iguales de 5 centímetros y una base de 4 centímetros, se dibuja primero la base. Luego, con el compás ajustado a 5 centímetros, se trazan arcos desde cada extremo de la base. La intersección de estos arcos marca el vértice opuesto a la base. Se unen los extremos de la base con este vértice para formar el triángulo isósceles, donde los dos lados resultantes miden 5 centímetros cada uno.
Construcción de un Triángulo Isósceles (Conociendo la Base y su Altura) [2:52]
Para construir un triángulo isósceles con una base de longitud no especificada y una altura de 4 centímetros, se dibuja primero la base. Se halla la mediatriz de la base para encontrar el punto medio, donde la altura debe ser perpendicular. Se traza una línea perpendicular desde este punto medio y se mide 4 centímetros sobre esta línea para determinar el vértice superior del triángulo. Finalmente, se unen los extremos de la base con este vértice para completar el triángulo isósceles.
Construcción de un Triángulo Rectángulo (Conociendo su Hipotenusa y un Cateto) [4:52]
Para construir un triángulo rectángulo con un cateto de 50 milímetros y una hipotenusa de 60 milímetros, se dibuja primero el cateto. En uno de los extremos del cateto, se levanta una perpendicular para formar el ángulo recto. Con el compás ajustado a 60 milímetros, se traza un arco desde el otro extremo del cateto hasta que corte la perpendicular. Este punto de intersección es el tercer vértice del triángulo. Se une este vértice con el extremo inicial del cateto para formar la hipotenusa, completando así el triángulo rectángulo.
Construcción de un Triángulo Escaleno (Conociendo la Altura y Dos Lados) [6:22]
Para construir un triángulo escaleno con una base de 30 milímetros, una altura de 40 milímetros y un lado de 60 milímetros, se dibuja primero la base. Se traza una línea perpendicular a la base para representar la altura. A 40 milímetros sobre esta perpendicular, se traza una línea paralela a la base. Con el compás ajustado a 60 milímetros, se traza un arco desde uno de los extremos de la base hasta que corte la línea paralela. Este punto de intersección es el tercer vértice del triángulo. Se une este vértice con los extremos de la base para completar el triángulo escaleno.
Dibujo de un Triángulo con Dos Lados y un Ángulo Conocidos [8:38]
Para dibujar un triángulo con dos lados de 55 milímetros cada uno y un ángulo dado, se dibuja primero uno de los lados (AB). Se transporta el ángulo dado al vértice A utilizando un compás para copiar el ángulo. Se mide 55 milímetros a lo largo del nuevo lado del ángulo y se marca el vértice C. Finalmente, se une el vértice C con el vértice B para completar el triángulo.