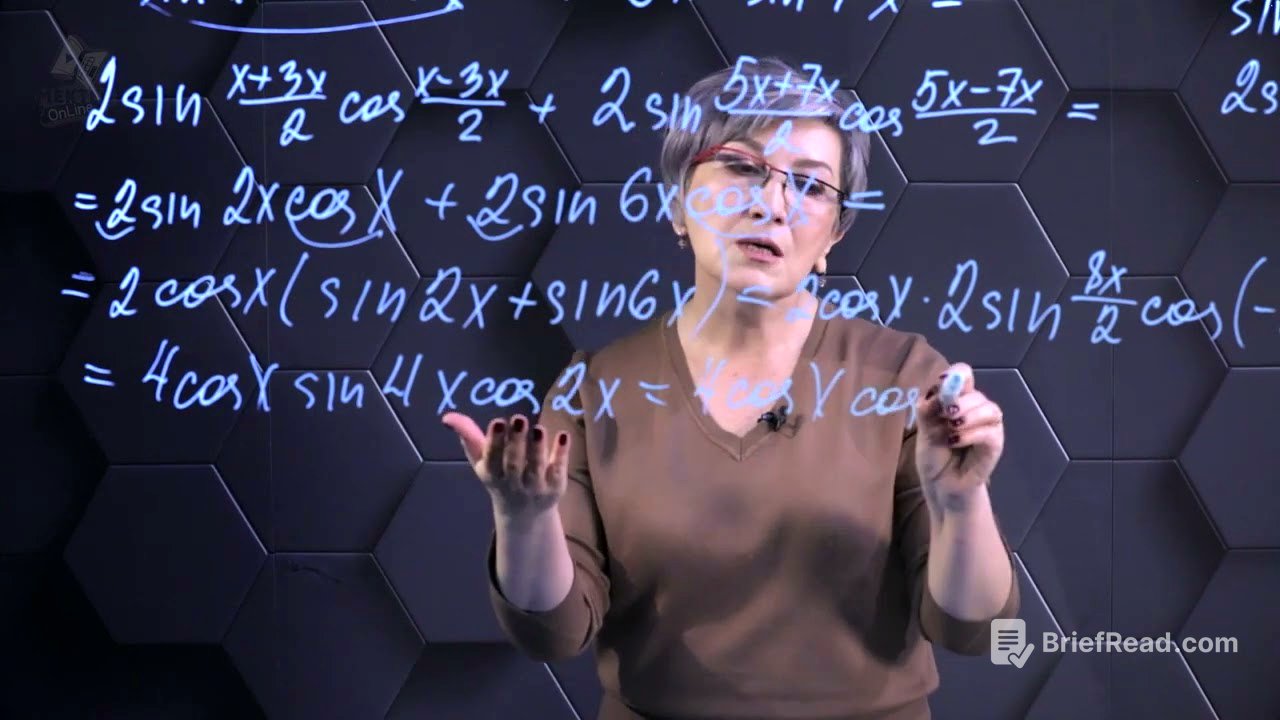Краткое содержание
В этом видеоуроке рассматривается упрощение тригонометрических выражений с использованием формул преобразования суммы синусов в произведение. Автор объясняет, как группировать слагаемые и применять формулы для упрощения выражений, а также показывает, что разные способы группировки могут привести к одному и тому же результату. Подчеркивается важность этих преобразований для решения тригонометрических уравнений, где необходимо приводить уравнение к одной тригонометрической функции и одному аргументу.
- Преобразование суммы синусов в произведение для упрощения выражений.
- Группировка слагаемых различными способами и получение одинакового результата.
- Применение формул косинуса суммы для дальнейшего упрощения.
- Важность упрощения тригонометрических выражений для решения уравнений.
Введение в преобразования тригонометрических выражений [0:08]
Автор приветствует зрителей и объявляет о продолжении темы преобразования тригонометрических выражений с целью их упрощения или нахождения значений. Подчеркивается, что для этого будут применяться различные тригонометрические формулы. Отмечается, что умение упрощать выражения необходимо для решения тригонометрических уравнений, где требуется привести уравнение к одной тригонометрической функции и одному аргументу.
Применение формулы суммы синусов [0:22]
Рассматривается выражение sin x + sin 3x + sin 5x + sin 7x, которое нужно преобразовать. Автор напоминает, что при упрощении выражений важно понимать, зачем это нужно. В данном случае, это необходимо для решения тригонометрических уравнений. Если в выражении нет двойного угла или его нельзя привести к двойному углу, то применяется формула суммы синусов: sin α + sin β = 2 sin((α + β)/2) * cos((α - β)/2).
Группировка слагаемых и упрощение выражения (Вариант 1) [2:19]
Автор объясняет, что при наличии четырех слагаемых их нужно сгруппировать. Сначала группируются первое и второе, а также третье и четвертое слагаемые. После применения формулы суммы синусов к каждой группе получается выражение 2 sin(2x) cos(-x) + 2 sin(6x) cos(-x). Учитывая, что cos(-x) = cos(x), выражение упрощается до 2 sin(2x) cos(x) + 2 sin(6x) cos(x). Затем выносится общий множитель 2 cos(x) за скобки, и получается 2 cos(x) (sin(2x) + sin(6x)).
Дальнейшее упрощение выражения с использованием формулы суммы синусов [5:01]
Для упрощения выражения в скобках (sin(2x) + sin(6x)) еще раз применяется формула суммы синусов. В результате получается 2 cos(x) * 2 sin(4x) cos(-2x). Учитывая, что cos(-2x) = cos(2x), выражение упрощается до 4 cos(x) sin(4x) cos(2x). Для более красивой записи множители переставляются по возрастанию углов: 4 cos(x) cos(2x) sin(4x).
Группировка слагаемых и упрощение выражения (Вариант 2) [6:37]
Автор показывает, что можно сгруппировать слагаемые по-другому: первое с четвертым, а второе с третьим. В этом случае получается выражение 2 sin(4x) cos(-3x) + 2 sin(4x) cos(-x). Учитывая, что cos(-x) = cos(x), выражение упрощается до 2 sin(4x) cos(3x) + 2 sin(4x) cos(x). Затем выносится общий множитель 2 sin(4x) за скобки, и получается 2 sin(4x) (cos(3x) + cos(x)).
Применение формулы суммы косинусов и сравнение результатов [8:03]
Для упрощения выражения в скобках (cos(3x) + cos(x)) применяется формула суммы косинусов: cos α + cos β = 2 cos((α + β)/2) * cos((α - β)/2). В результате получается 2 sin(4x) * 2 cos(2x) cos(x), что упрощается до 4 sin(4x) cos(2x) cos(x). Автор подчеркивает, что, несмотря на разную группировку слагаемых, результат получился тем же самым, что и в первом варианте.
Заключение [9:06]
Автор сообщает, что на следующем занятии будет рассмотрен еще один прием упрощения тригонометрических выражений, и прощается со зрителями.