Breve Resumen
Este video explica las cardioides, figuras definidas mediante coordenadas polares. Se revisan conceptos básicos de coordenadas polares y su conversión a rectangulares, destacando la representación no única de puntos en polares. Se exploran ejemplos de ecuaciones de cardioides, como r = 1 + cos(θ), y cómo modificar la ecuación afecta la forma de la figura, incluyendo la creación de formas de "almeja" y bucles internos al variar los parámetros. También se muestra cómo la función seno produce cardioides orientadas verticalmente.
- Las cardioides son figuras con forma de corazón definidas en coordenadas polares.
- La ecuación r = a + b cos(θ) determina la forma de la cardioide, donde 'a' y 'b' son constantes.
- Variar los parámetros en la ecuación puede crear diferentes formas, como "almejas" o figuras con bucles internos.
Recordatorio de Coordenadas Polares [0:30]
Se hace un repaso de las coordenadas polares como alternativa a las coordenadas rectangulares. Se recuerdan las fórmulas para convertir entre coordenadas polares y rectangulares. Se menciona que en coordenadas polares, cada punto tiene múltiples representaciones, lo que puede complicar las ecuaciones. Se establecen convenciones para trabajar con coordenadas polares, especialmente en el origen, donde pueden surgir problemas. Generalmente, la distancia al polo (r) se expresa como una función del ángulo (θ), a menudo utilizando funciones trigonométricas. El valor de 'r' puede ser negativo, lo que indica que el punto se encuentra en la dirección opuesta al ángulo.
Cardioide: r = 1 + cos(θ) [1:48]
Se presenta el ejemplo clásico de una cardioide: r = 1 + cos(θ). Se explica que la función coseno varía entre -1 y 1, por lo que 'r' varía entre 0 y 2. La gráfica resultante tiene forma de corazón, con simetría horizontal. El punto más alejado del origen está a una distancia de 2, cuando el ángulo es 0, y el punto más cercano está en el origen, cuando el ángulo es π.
Variaciones de la Ecuación: r = a + cos(θ), a > 1 [2:50]
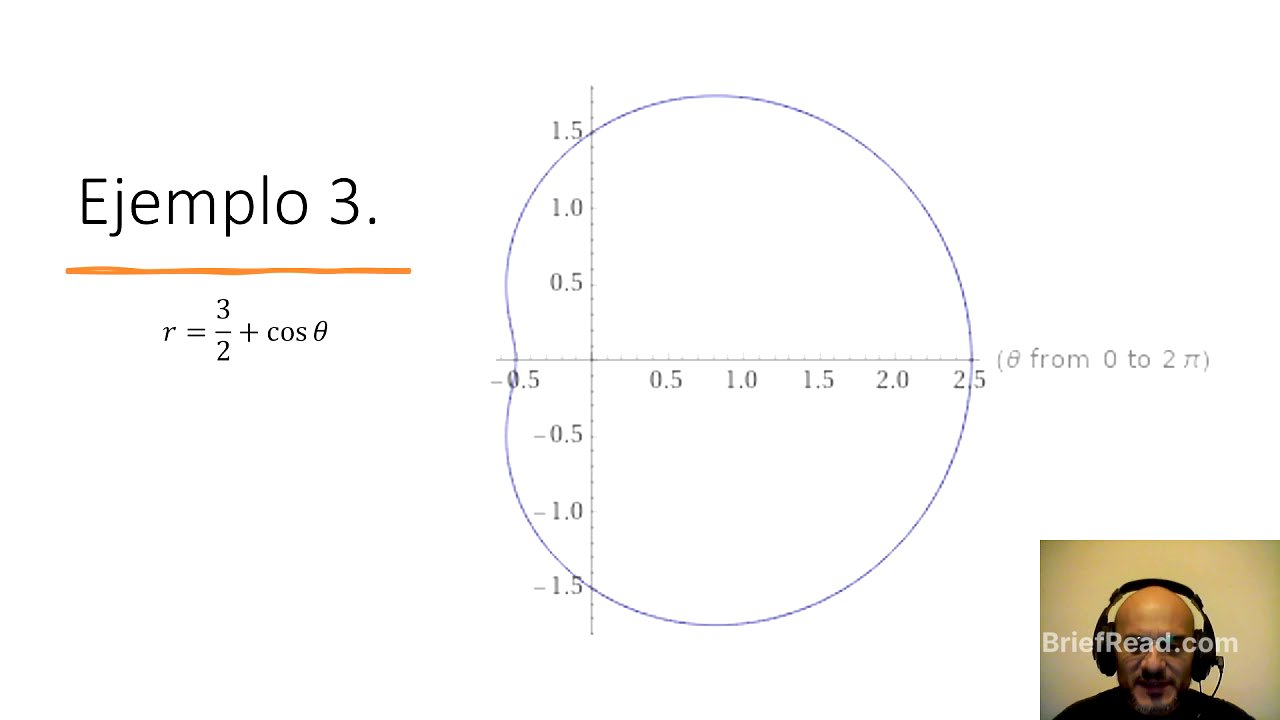
Se explora qué sucede cuando se modifica la ecuación a r = 2 + cos(θ). En este caso, la figura resultante no es una cardioide, sino una forma más redondeada. Como el coseno varía entre -1 y 1, 'r' varía entre 1 y 3. A medida que el valor constante sumado al coseno es mayor, la forma se vuelve más circular. Se introduce el término "almeja" para describir la forma que se obtiene con r = 1.5 + cos(θ), donde se observa una hendidura en el lado izquierdo de la figura.
Valores Negativos de r: r = -0.5 + cos(θ) [4:30]
Se analiza el caso donde la constante sumada al coseno es negativa: r = -0.5 + cos(θ). Aquí, 'r' puede tomar valores negativos, lo que resulta en la creación de un bucle interno en la figura. Este bucle se forma cuando 'r' es negativo para ciertos ángulos. Se explica que los valores negativos de 'r' indican que el punto se grafica en la dirección opuesta al ángulo.
r = -1 + cos(θ) [5:42]
Se muestra que la ecuación r = -1 + cos(θ) genera la misma figura que r = 1 + cos(θ), pero con todos los valores de 'r' negativos. Esto significa que cada punto se grafica en la dirección opuesta, pero la forma final es idéntica.
Cardioides con la Función Seno: r = 1 + sen(θ) [6:39]
Se introduce la función seno en la ecuación: r = 1 + sen(θ). Se explica que la cardioide resultante es similar a la obtenida con el coseno, pero orientada verticalmente. Se menciona que se pueden realizar desplazamientos y cambios de fase para modificar la orientación y forma de la cardioide. Se concluye que al sumar una constante a las funciones seno o coseno, se pueden crear diversas formas, manteniendo la esencia de la cardioide.