TLDR;
This video provides a detailed explanation of Coulomb's Law, including its formula, key concepts, and applications. It covers the relationship between electric force, charge, and distance, and compares electric force to gravitational force. The video also includes several example problems, starting with simple two-charge scenarios and progressing to more complex three-charge configurations, including both collinear and non-collinear arrangements. The presenter explains how to calculate the net force and direction in these scenarios, incorporating vector addition and trigonometric principles.
- Coulomb's Law describes the electric force between charged objects.
- Electric force is directly proportional to the magnitude of the charges and inversely proportional to the square of the distance between them.
- The video includes example problems with detailed solutions for various charge configurations.
Introduction to Coulomb's Law [0:12]
The lesson introduces Coulomb's Law as a fundamental principle in electrostatics, explaining that it quantifies the force between two point charges separated by a distance. It recaps basic electrostatic concepts, such as like charges repelling and unlike charges attracting. The magnitude of these attractive or repulsive forces can be calculated using Coulomb's Law.
Formula and Components of Coulomb's Law [1:22]
The formula for Coulomb's Law is presented as F = k * (q1 * q2) / r^2, where F is the force, k is Coulomb's constant (9 x 10^9 Nm²/C²), q1 and q2 are the magnitudes of the charges, and r is the distance between the charges. The unit for charge is Coulombs (C), and the unit for distance is meters (m). The resulting force is measured in Newtons (N). An illustration shows two charges, q1 and q2, separated by a distance 'r', with arrows indicating attraction when charges are opposite and repulsion when charges are the same.
Electric vs. Gravitational Force and Proportionality [3:47]
The electric force is much stronger than the gravitational force. The force between two charges gets stronger as the charges move closer together, indicating an inverse relationship between force and distance. The force also increases if the amount of charge becomes larger, showing a direct relationship between force and charge magnitude. The force is directed along the line connecting the centers of the charges and always occurs in pairs, consistent with Newton's third law.
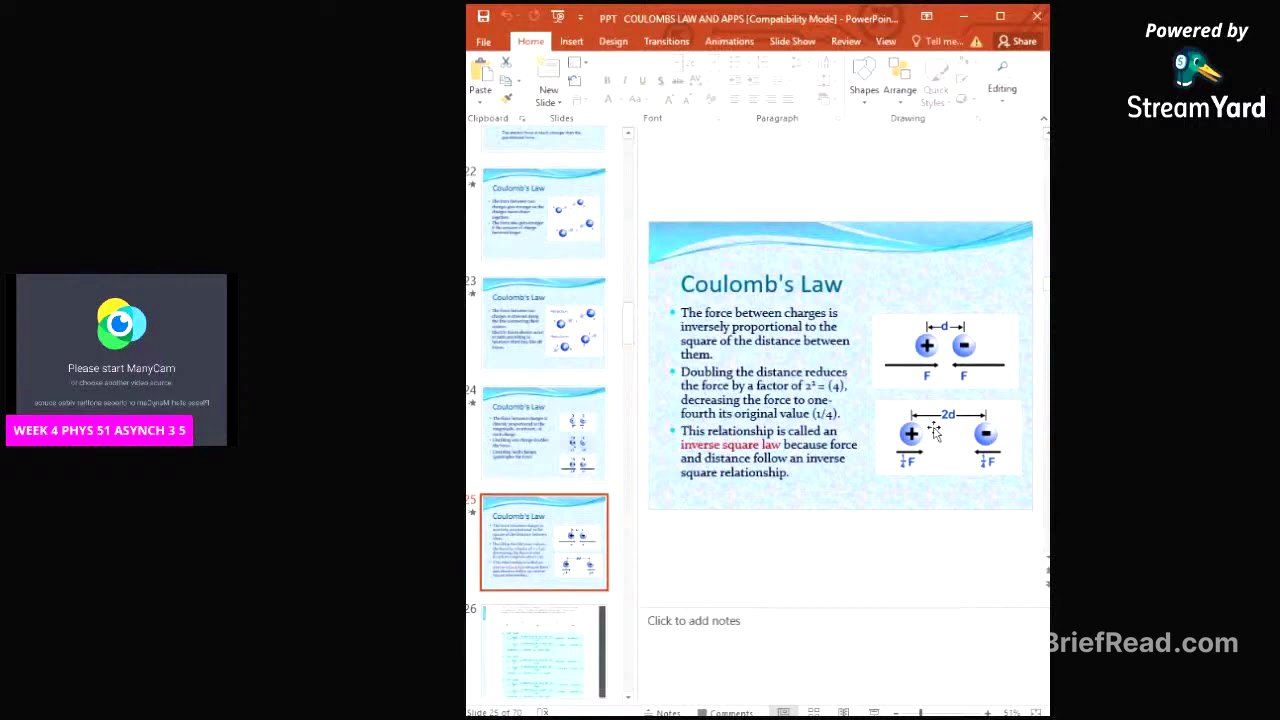
Direct and Inverse Proportionality in Coulomb's Law [7:50]
The force between charges is directly proportional to the magnitude of each charge. Doubling one charge doubles the force, while doubling both charges quadruples the force. The force is inversely proportional to the square of the distance between the charges. Doubling the distance reduces the force by a factor of four, which is known as the inverse square law.
Calculating Electric Force: Example 1 [10:49]
Two balls each have a static electric charge of 0.001 C and are separated by 0.1 meters. The force between them is calculated using Coulomb's Law: F = (9 x 10^9 Nm²/C²) * (0.001 C * 0.001 C) / (0.1 m)². The result is 9,000 N. This force is then compared to the weight of a 70 kg person, which is 686 N (calculated as mass times gravity, 70 kg * 9.8 m/s²). The electric force is approximately 13 times the weight of the average person.
Impact of Distance and Charge on Electric Force [14:23]
If the distance between two charges is doubled, the force becomes one-fourth of the original force. If one of the charges is doubled, the force doubles. If both charges are doubled and the distance is halved, the force becomes 16 times the original force.
Comparing Gravitational and Electric Forces: Example 2 [15:37]
Two 40-gram masses, each with a charge of 3 micro Coulombs, are placed 50 cm apart. The gravitational force and the electric force between them are compared. The gravitational force is calculated using FG = G * (m1 * m2) / r^2, where G is the gravitational constant (6.67 x 10^-11 Nm²/kg²), m1 and m2 are the masses (0.04 kg each), and r is the distance (0.5 m). The electric force is calculated using Coulomb's Law. The electric force (0.324 N) is significantly greater than the gravitational force (4.27 x 10^-13 N), proving that the electric force is much stronger.
Calculating Electric Force: Example 3 [29:29]
Two charged particles, qp = 10 micro Coulombs and qq = 20 micro Coulombs, are separated by 12 cm. The magnitude of the electrostatic force is calculated using Coulomb's Law. The force is found to be 125 N.
Calculating Electric Force: Example 4 [40:08]
A charge of 2 Coulombs is 1.5 meters away from a charge of -3 Coulombs. The force they exert on each other is determined using Coulomb's Law. The result is -24 x 10^9 N, indicating an attractive force due to the opposite signs of the charges.
Net Force with Three Charges in a Line [42:51]
The video transitions to scenarios involving three charges arranged in a line, emphasizing the importance of considering both magnitude and direction. The net force on a charge is the vector sum of the forces from the other two charges. The presenter explains how to determine the direction of the forces based on the signs of the charges and how to use positive and negative signs to represent direction.
Net Force on a Charge: Example 5 [44:46]
Three charges are arranged in a line, and the net force acting on the charge on the right (qc) is determined. The force from charge a to c (fac) and the force from charge b to c (fbc) are calculated separately using Coulomb's Law. The net force is the sum of these two forces, taking direction into account. The final net force is 0.201 N to the right.
Non-Collinear Charges and Pythagorean Theorem [1:05:19]
The video introduces non-collinear charges, where the charges are not arranged in a straight line. If the charges form a right triangle, the Pythagorean theorem can be applied to find the net force. The Pythagorean theorem states that c^2 = a^2 + b^2, where c is the hypotenuse and a and b are the other two sides of the right triangle.
Finding Angles and Sides in Right Triangles [1:06:53]
The video reviews how to find missing sides and angles in a right triangle. To find a missing side, rearrange the Pythagorean theorem. To find an angle, use trigonometric functions such as tangent (tan), where tan(θ) = opposite / adjacent.
Net Force with Non-Collinear Charges: Example 6 [1:14:33]
Three charges are arranged in a right angle, and the force on q2 is determined. The forces between q1 and q2 and between q2 and q3 are calculated using Coulomb's Law. The net force is found using the Pythagorean theorem, and the angle is found using the arctangent function. The final net force is approximately 3 x 10^9 N, and the angle is approximately 48 degrees.