TLDR;
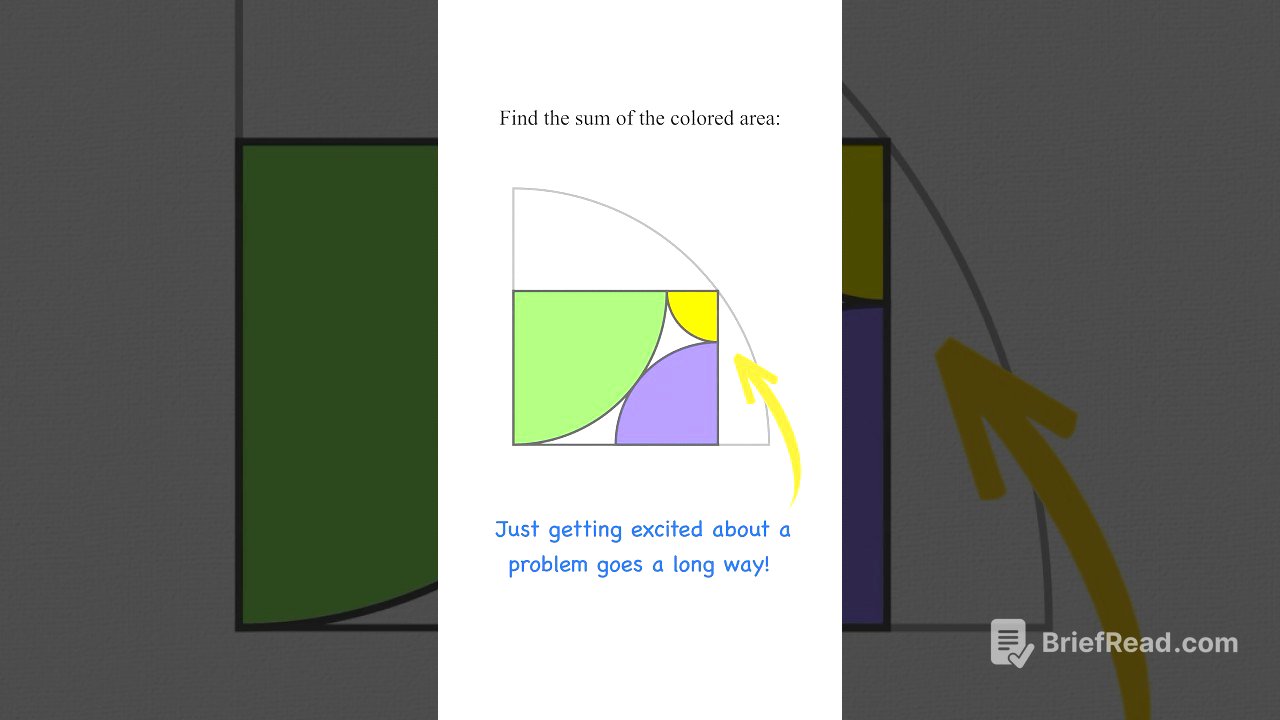
The video presents a geometry problem involving three quarter circles inscribed within a larger one. The goal is to find the total colored area, given that the radius of the smallest (yellow) circle is 1. The problem is solved by determining the radii of the other two circles (violet and green) using geometric relationships and the Pythagorean theorem. The solution involves setting up a quadratic equation, solving for the unknown radius, and then calculating the areas of the quarter circles to find their sum.
- The radii of the three circles are found to be 1, 2, and 3.
- The sum of the areas of the three quarter circles is 7π/4.
Problem Setup and Initial Radii [0:00]
The problem features three quarter circles inscribed inside a larger circle. The radius of the yellow quarter circle is given as 1, and the radius of the violet quarter circle is assumed to be x. The objective is to find the total colored area of the three quarter circles.
Geometric Relationships and Rectangle Formation [0:13]
Since all three shapes are quarter circles, their centers form a rectangle. One side of this rectangle is equal to the sum of the radii of the violet and yellow circles (x + 1), which is also the radius of the green circle. The adjacent side of the rectangle is the sum of the radii of the green and yellow circles, which simplifies to x + 2.
Applying the Pythagorean Theorem [0:35]
The diagonal of the rectangle is the sum of the radii of the violet and green circles, expressed as 2x + 1. By applying the Pythagorean theorem to the rectangle, a quadratic equation is derived.
Solving for x and Determining Radii [0:43]
Solving the quadratic equation yields x = 2. This means the radii of the three circles are 1 (yellow), 2 (violet), and 3 (green).
Calculating the Total Colored Area [0:52]
The sum of the areas of all three quarter circles is calculated using the radii found. The total colored area is determined to be 7π/4.