TLDR;
This video provides a detailed explanation of single-variable calculus, focusing on topological notions, metrics, and metric spaces. It explains the importance of calculus in science and engineering, introduces topology as the study of figures that can be deformed, and defines metrics as distance functions between points in a metric space. The video also covers the properties required for a space to be considered a metric space, including positivity, commutativity, and the triangle inequality, and includes examples and exercises.
- Calculus is essential for science and engineering.
- Topology studies figures that can be deformed.
- Metrics are distance functions in metric spaces.
- Metric spaces must satisfy positivity, commutativity, and the triangle inequality.
Introduction [0:00]
The instructor introduces a remake of the single-variable calculus playlist with enhanced content and more exercises. The goal is to improve and expand the existing material. Before starting, the instructor emphasizes the importance of understanding what calculus is.
Why Study Calculus? [0:46]
Calculus is fundamental to science and engineering. It is described as the backbone of these fields, essential for various disciplines including economics, biology, and all engineering fields. Calculus is defined as the branch of mathematics that studies change, particularly how one variable changes with respect to another, which is known as the derivative.
Topological Notions [1:45]
The initial topic is topological notions, which are essential for understanding calculus. Topology is similar to geometry but deals with figures that can be deformed, stretched, or have holes made in them, unlike the rigid figures studied in geometry. Topology provides the mathematical basis for concepts like limits, which are defined based on metric spaces.
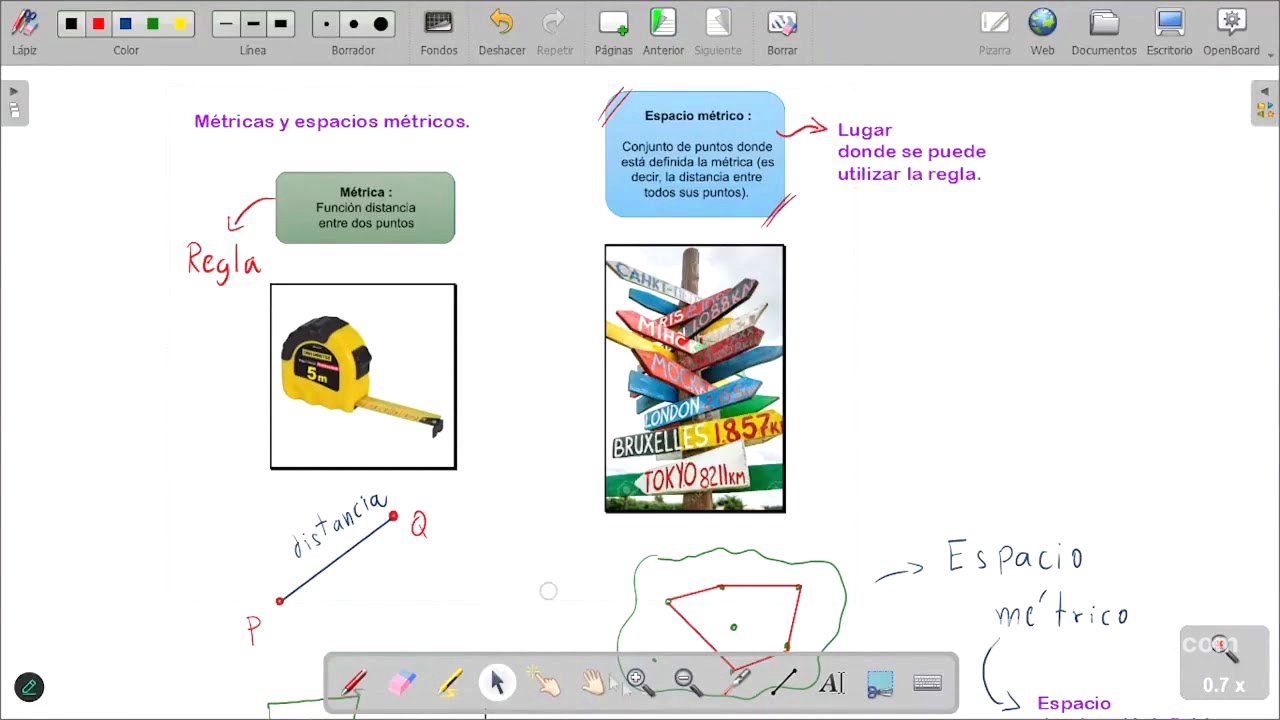
Metrics and Metric Spaces [3:51]
A metric is defined as a distance function between two points, while a metric space is a set of points where the metric can be used. The metric helps determine the distance between two points, P and Q, in a space such as R1, R2, or R3. Metric space is where the concept of distance between two points is defined. The metric is the rule, and the metric space is the place where you can use the rule.
Requirements for Metric Space [7:27]
To determine if something is a metric space, three requirements must be checked:
- If P is different from Q, the distance between P and Q is greater than 0; if P equals Q, the distance between them is 0.
- Commutativity: the distance from P to Q is the same as the distance from Q to P.
- The triangle inequality: the distance from P to Q is less than or equal to the distance from P to R plus the distance from R to Q.
All three requirements must be met for a space to be considered a metric space.
Exercise: Verifying Metric Space Properties [13:29]
An exercise is presented to determine if a given space, defined by the absolute value of x - y, is a metric space. The three requirements are checked:
- The distance from X to Y is greater than 0 if X is different from Y, which is true due to the nature of absolute value.
- If X equals Y, the distance from X to Y is 0, which is also true.
- The commutative property is verified using algebraic manipulation and properties of absolute values.
- The triangular inequality is confirmed by referencing properties of absolute values learned in pre-calculus.
Since all three properties are fulfilled, the space is a metric space.
Exercise: Proving or Disproving Metric Space [23:34]
Another exercise asks to prove if a space defined by the absolute value of the sine of x minus the sine of y is a metric space. A counterexample is used to show that the positivity requirement is not always met, as the sine function can result in zero even when x and y are different. Therefore, the space is not a metric space.
Exercise: Checking Properties Separately [30:03]
This exercise involves checking if a function satisfies the positivity property and the triangle inequality property separately. It is shown that while the positivity property is always fulfilled due to the absolute value and squaring, the triangle inequality is not. A counterexample demonstrates that the inequality does not hold for all real numbers, thus the space is not a metric space.
Identifying Metric Axioms That Don't Hold [42:35]
The task is to identify which metric axioms do not hold for given functions. For the function d(x, y) = (x - y)³, it is shown that the positivity property is not met because the result can be negative. For a piecewise function, it is demonstrated that the commutative property does not hold.
Elements of Metric Spaces: Environment (Neighborhood) [51:38]
The concept of the environment, also known as the neighborhood or ball, is introduced. The environment is represented as N sub R of P, where P is the center and R is the radius. An example is provided to show how to represent and graph an environment on the real line.
Example: Representing and Graphing an Environment [53:52]
An example demonstrates how to solve an inequality with absolute value to represent an environment on the real line. The center and radius are identified, and the interval is graphed.
Example: Environment with Negative Radius [58:11]
An example shows that an environment with a negative radius has no solution because the radius cannot be negative.
Non-Included Environment [1:00:35]
The concept of the non-included environment is introduced, which is similar to the previous one but excludes the center. The notation and definition are explained, and an example is provided to show how to solve and represent a non-included environment on the real line.
Open Ball and Reduced Open Ball [1:06:12]
The concepts of the open ball and reduced open ball are introduced. The open ball is the same as the environment, while the reduced open ball is similar to the non-included environment but may not always involve an absolute value.
Exercise: Representing Open and Reduced Open Balls [1:08:35]
An exercise involves representing open balls and reduced open balls as inequalities with absolute value and graphically on the real line. The Euclidean metric is introduced as the default metric when no specific function is given.
Applying the Euclidean Metric [1:11:42]
The Euclidean metric is applied to solve for the open ball, and the interval is graphed. The center and radius are identified on the graph.
Solving for Open Ball [1:15:22]
Another open ball is solved for, and the interval is graphed. The center and radius are again identified on the graph.
Solving for Reduced Open Ball [1:19:02]
The reduced open ball is solved for, and the interval is graphed. The center is excluded from the interval.
Solving for Reduced Open Ball Graphically [1:22:36]
The last reduced open ball is solved for graphically, without doing the calculation. The center and radius are used to determine the interval, and the center is excluded.