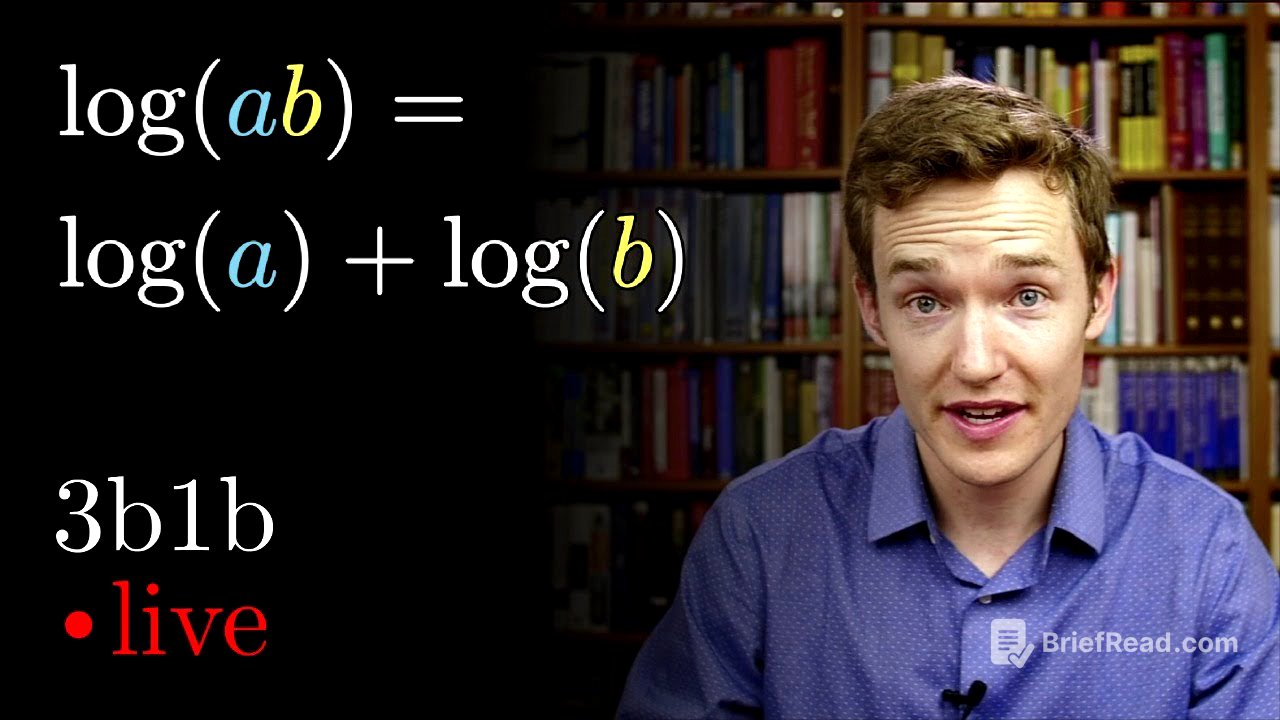TLDR;
This video explains logarithms, their properties, and their applications. It begins by illustrating how logarithmic scales are used to visualize exponential growth, such as in the early stages of a pandemic. The video then addresses the fundamental question of what logarithms actually are, explaining them as the inverse of exponentiation. It covers key logarithmic properties, including how logarithms transform multiplication into addition and how to change the base of a logarithm. The lecture uses practice problems and real-world examples, such as the Richter scale for earthquakes, to build intuition and understanding.
- Logarithms are the inverse of exponentiation, useful for understanding multiplicative relationships.
- Key properties include log(A*B) = log(A) + log(B) and the change of base formula.
- Logarithmic scales are used to represent phenomena with wide-ranging values, like earthquake magnitudes.
Introduction to Logarithmic Scales [0:00]
The video starts by discussing how logarithmic scales are used to visualize exponential growth, particularly in the context of phenomena like the spread of a virus. It explains that while exponential curves can be difficult to interpret on a linear scale, using a logarithmic y-axis, where each step represents multiplication rather than addition, makes it easier to project trends. An example from a previous video about the early stages of the pandemic is referenced, where a naive exponential model surprisingly accurately predicted the number of cases. The presenter notes that logarithms are helpful in understanding multiplicative increases in various natural and man-made contexts.
Defining Logarithms and Their Inverse Relationship [6:47]
The video addresses the question of what logarithms actually are by explaining their inverse relationship to exponentiation. Using the example of 10^3 = 1000, it shows that this relationship can be expressed in three ways: exponentiation, nth rooting, and logarithms. The presenter references a previous video that introduced an alternate notation using a triangle to represent the relationship between the base, exponent, and result. Logarithms are presented as the inverse operation that finds the exponent when the base and result are known, distinguishing them from radicals, which find the base.
Logarithm Notation and Conventions [16:42]
The discussion covers the conventions of logarithm notation, clarifying that "log" without a specified base will initially refer to log base 10 for the sake of intuition. It is mentioned that in mathematics, "log" often implies log base e (natural logarithm), while in computer science, it typically means log base 2. The presenter emphasizes that understanding logarithms involves recognizing that the logarithm of a value represents the exponent to which the base must be raised to obtain that value.
Property 1: Logarithm of a Product [19:47]
The first property of logarithms, log(A * B) = log(A) + log(B), is introduced through a practice problem. The problem asks viewers to identify the correct expression for log(1000 * x). The solution involves plugging in powers of 10 for x and recognizing that multiplying powers of 10 results in adding their exponents (or, equivalently, adding the number of zeros). This illustrates that the logarithm of a product is the sum of the logarithms of the individual factors.
Property 2: Logarithm of a Power [25:12]
The video introduces the property log(x^n) = n * log(x) through another practice problem. Viewers are asked to identify the correct expression for log(x^n). The solution involves considering x^n as repeated multiplication of x and applying the first property to break it down into a sum of logarithms. This leads to the conclusion that the exponent n can be brought down as a coefficient, simplifying the expression. The presenter also notes the mirror image exponential property: (10^x)^n = 10^(n*x).
Property 3: Change of Base [31:55]
The change of base property is explained, addressing what happens when the base and the argument inside the logarithm are swapped. The correct answer is log base a of b is 1 divided by log base b of a. This is demonstrated through the example of log base 10 of 1000 and log base 1000 of 10. The presenter relates this property to the corresponding exponential rule and emphasizes the importance of thinking of logarithms as turning exponentiation inside out.
Why Log(a+b) Doesn't Simplify [37:40]
The video addresses a common misconception by demonstrating that log(a + b) does not have a simple, general property. Through a quiz question and examples using powers of 10, it's shown that adding the inputs of a logarithm does not result in a straightforward simplification. The presenter emphasizes the importance of recognizing when a logarithmic expression cannot be easily simplified.
Real-World Example: The Richter Scale [45:59]
The lecture uses the Richter scale for earthquakes as a real-world example of logarithms. It explains that the Richter scale quantifies the strength of an earthquake, and each step on the scale corresponds to a multiplicative increase in energy released. For instance, a one-unit increase on the Richter scale corresponds to roughly a 32-fold increase in energy. The presenter highlights how logarithmic scales are used to represent phenomena with a wide range of values, such as earthquake sizes or sound intensities (decibel scale).
Approximating Logarithms with Different Bases [55:25]
The discussion shifts to how logarithms with different bases can be approximated and related to each other. Using the approximation that 2^10 ≈ 1000, the video demonstrates how to estimate log base 2 of 10 and log base 10 of 2. It's shown that log base 10 of 2 is approximately 0.3, and this relationship is used to estimate logarithms of other powers of 10. The presenter emphasizes that numbers described with one base are basically the same as describing them with another base, but there's some rescaling constant.
Change of Base Formula [1:05:31]
The change of base formula is presented as a way to convert logarithms from one base to another. The formula states that log base b of a can be computed using any other base c as log base c of a divided by log base c of b. An example is given using log base 100 of a million, which is computed using log base 10. The presenter explains that this formula is important because it allows computations using a common base, such as the natural logarithm (log base e).
Applying Change of Base [1:16:02]
The presenter reinforces the change of base concept with another quiz question. Given the approximation that log base 2 of 10 is around 10/3, viewers are asked to identify the correct relationship between log base 2 of x and log base 10 of x. The solution involves using the change of base formula to convert log base 2 to log base 10, demonstrating that log base 2 of x is approximately (10/3) * log base 10 of x.
Challenge Problem: Simplifying a Sum of Logarithmic Fractions [1:23:58]
The video concludes with a challenge problem involving the simplification of a sum of fractions with logarithms of factorials in the denominators. The problem requires using the change of base formula to rewrite the fractions with a common denominator. Then, the property of logarithms that turns products into addition is used to simplify the numerator. This leads to the cancellation of terms and a final answer of 1.