TLDR;
This video explains how to determine the bounds of a triple integral by describing the 3D space and using the method of collapsing. It covers how to choose a variable to move through the region, describe the surfaces entered and exited, and collapse the region onto the remaining axes. The video also demonstrates how the order of variables doesn't matter as long as the function is continuous, but choosing the right order can simplify the bounds.
- Triple integrals calculate hypervolume or volume of a 3D region.
- The method of collapsing simplifies finding bounds by reducing the dimensions step by step.
- The order of integration can be chosen to simplify the bounds.
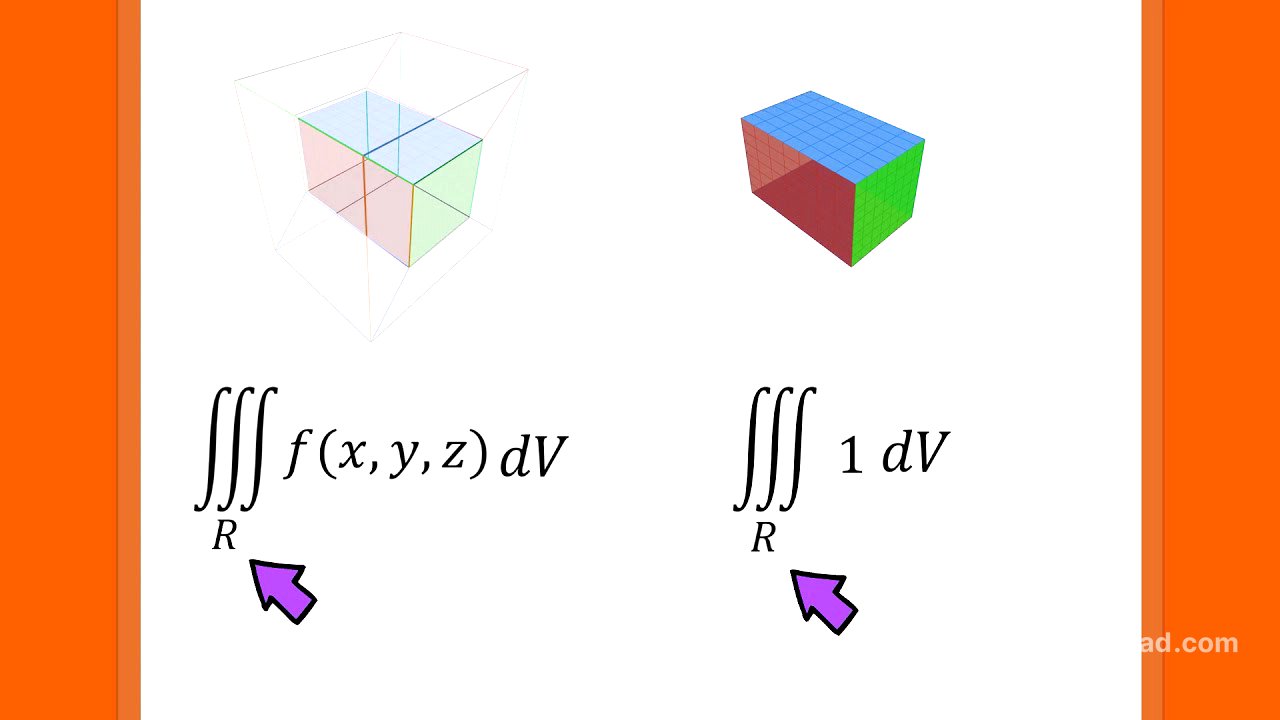
What does a triple integral describe? [0:05]
A triple integral, when applied to a function, calculates a hypervolume, which is the volume bounded by a three-dimensional region and the surface of the function. If the triple integral is applied to a function that equals 1, it calculates the volume of the three-dimensional region itself. The bounds of the triple integral define the three-dimensional space being considered.
The method of collapsing [0:38]
The method of collapsing involves choosing a variable or direction to move through the three-dimensional region. As you move through the region, identify the surfaces you enter and exit. These surfaces, described by functions, become the bounds of the integral associated with the chosen direction. The region then collapses onto the remaining axes, and the process is repeated for the remaining variables.
The bounding surfaces of the region [1:12]
The region is bounded by three surfaces: a top plane defined by z = y + 1, a bottom parabolic cylinder defined by z = x^2 + 1, and a side plane defined by y = 1. These surfaces define the three-dimensional space for which the triple integral will be calculated.
Example 1, dzdydx [1:29]
To find the bounds, the region is first traversed in the z-direction, entering through the parabolic cylinder (z = x^2 + 1) and exiting through the plane (z = y + 1). This establishes the z-bounds as x^2 + 1 to y + 1. The region is then collapsed onto the x-y plane, and the y-direction is chosen next. The region is entered at the parabola y = x^2 and exited at the line y = 1, setting the y-bounds as x^2 to 1. Finally, collapsing onto the x-axis, the region is entered at x = -1 and exited at x = 1, giving the x-bounds.
Example 2, dydxdz [2:49]
The region is traversed in the y-direction, entering at the slanted plane z = y + 1 and exiting at the plane y = 1. Solving for y, the y-bounds are z - 1 to 1. The region is then collapsed onto the x-z plane, and the x-direction is chosen. The region is entered at the left of a parabola and exited at the right of a parabola, described by z = x^2 + 1. Solving for x, the x-bounds are -sqrt(z - 1) to sqrt(z - 1). Collapsing onto the z-axis, the region is entered at z = 1 and exited at z = 2, giving the z-bounds.
A note on keeping bounds simple [4:15]
While the order of variables does not affect the result if the function is continuous, choosing the order carefully can simplify the bounds. Simpler bounds make the integral easier to evaluate.
Wrap up information and ending [4:28]
The video concludes by encouraging viewers to like the video, subscribe to the channel, and visit MySecretMathTutor.com for more examples and organized content.