TLDR;
This video explains the concept of search algorithms in computational thinking, focusing on linear search and binary search. It details how these algorithms work, their efficiency, and when to use them, providing examples to illustrate each method. The key takeaway is understanding how search algorithms optimize the process of finding specific data within a larger set, improving speed and efficiency.
- Introduces the concept of search algorithms for efficiently finding data.
- Explains linear search (sequential search) and binary search algorithms.
- Provides step-by-step examples of how each algorithm works.
- Highlights the importance of using appropriate search strategies for different data sets.
Introduction to Search Algorithms [0:01]
The video introduces the concept of searching as finding specific elements within a set of data. A search is successful if the element is found and unsuccessful otherwise. In informatics, searching involves finding an object that meets certain criteria from a collection of objects of the same data type. The process involves comparing the value being searched for with the existing data. For example, finding a book involves comparing each book title until a match is found. When dealing with large datasets, a search strategy is needed to ensure the process is fast, precise, and efficient, using minimal resources.
Linear Search (Sequential Search) [6:01]
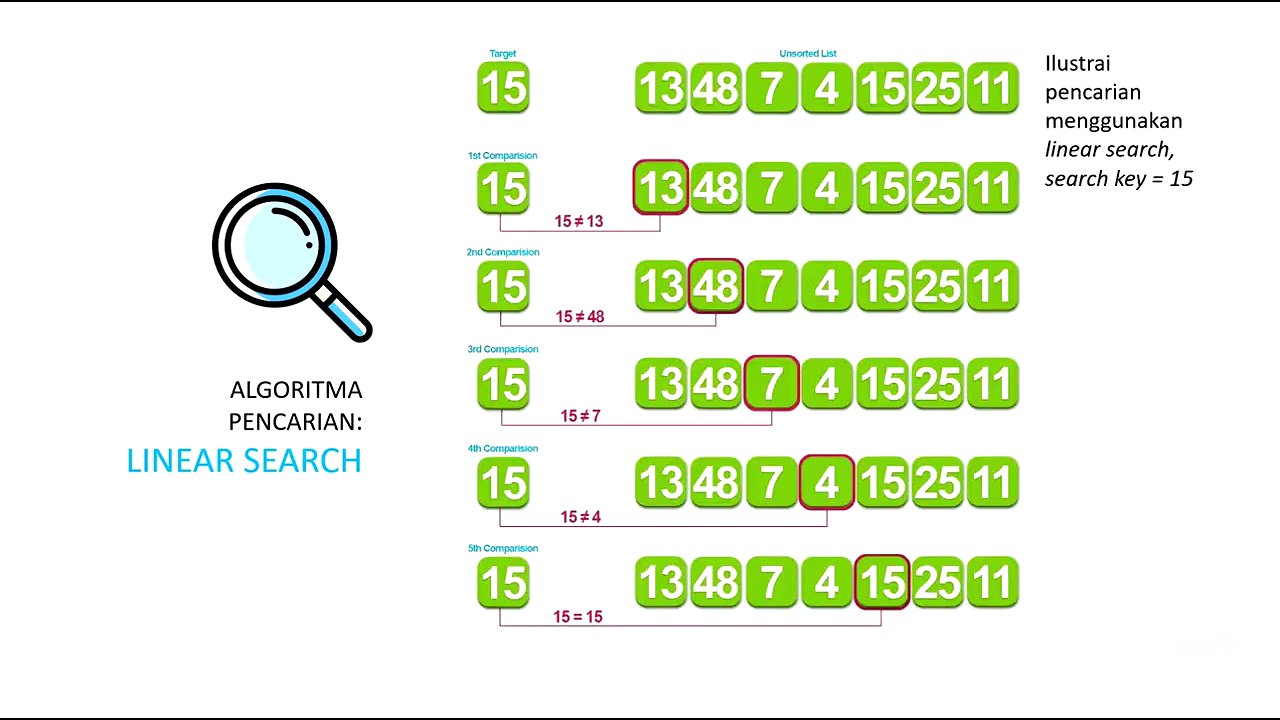
Linear search, also known as sequential search, involves comparing the data being searched for with each data point in the list, one by one, starting from the front or back. The search continues until a match is found or the end of the data is reached. If the data is not found by the end, the search is declared unsuccessful. This algorithm is typically used for unordered lists. The steps include starting, determining the data being searched, comparing it with the first data point, and repeating the comparison with subsequent data points until a match is found or the end is reached.
Linear Search Example [7:58]
To illustrate linear search, the video uses a list of random numbers: 13, 48, 7, 4, 15, 25, and 11. The goal is to find the number 15. The algorithm compares 15 with each number in the list sequentially: 13, 48, 7, and 4, until it reaches 15, at which point the search is successful. This demonstrates how each element is compared one by one until the desired value is found.
Binary Search (Half Interval Search) [10:08]
Binary search, also known as half interval search, involves comparing the value being searched for with the middle value (median) of the dataset. If the value doesn't match, the algorithm eliminates half of the data where the target value cannot be located and repeats the process on the remaining half. This continues until the data is found or the dataset can no longer be divided. Binary search is typically used for sorted data. The algorithm starts by determining the data being searched, comparing it with the median, and eliminating the irrelevant half based on whether the target is larger or smaller than the median.
Binary Search Example [12:38]
The video demonstrates binary search using a sorted list of 10 numbers. Each number is indexed from 1 to 10 to simplify the process. The goal is to find the number 31. The median is determined by adding the first and last indices (1 + 10) and dividing by two, resulting in 5.5, which is rounded to 5. The value at index 5 is 27. Since 31 is greater than 27, the algorithm eliminates all numbers less than or equal to 27. The process repeats with the remaining numbers until 31 is found.
Additional Binary Search Examples and Conclusion [17:57]
The video references additional examples of binary search on subsequent slides, reinforcing the process of finding the middle value, comparing, and eliminating until the data is found or the search is exhausted. The conclusion emphasizes that search algorithms prevent the need to examine all data points, using strategies to focus the search and efficiently locate the desired information. By using search strategies, not all data needs to be checked, making the process more efficient.