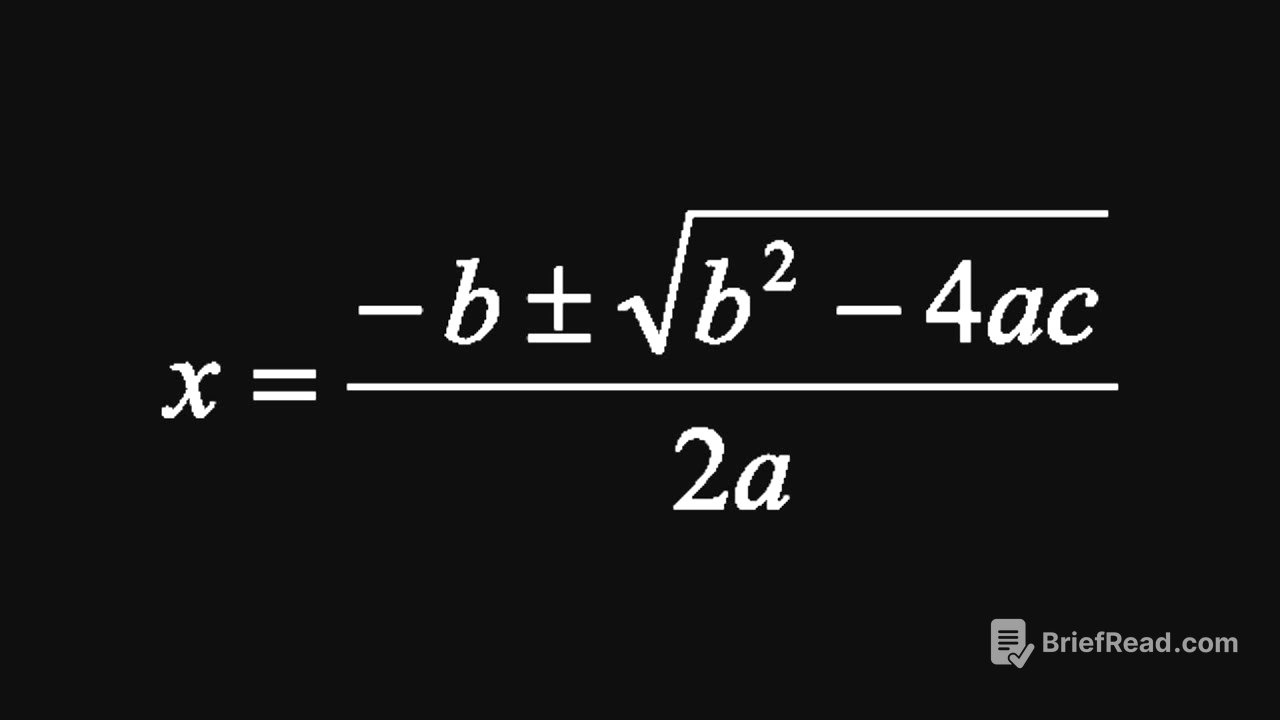Math Expressions in C | Part 2

Brief Summary

This video is about continuing a C project named "proof," a simple language for proving math statements. The creator implemented the lexer and parser, enabling the parsing of defines, variables, functions, and operators. The language consists of statements that can be definitions, expressions, or equalities, including defining sets, functions, and operators with rules. The goal is to define statements and prove simple statements step by step. The video covers implementing the parse_equality function, handling operator precedence, and parsing different types of equalities such as sets and expressions.

• Implemented lexer and parser for the "proof" language.
• Parsing defines, variables, functions, and operators.
• Implementing parse_equality function and handling operator precedence.

Intro and Project Overview

The creator is continuing with the C project, now named "proof," which is designed as a simple language for proving mathematical statements. The project has implemented the lexer and most of the parser, allowing it to parse definitions, variables, functions, and operators. The language is statement-based, where each statement can be a definition or an equality, and can include both. The language aims to define sets, functions, and operators, along with rules for these functions, to prove mathematical statements step by step.

Language Structure and Examples

The language consists of statements that can define sets, such as a set of numbers, or built-in infinite sets. It also includes defining functions and operators, and adding rules for these functions, which are treated as true axioms. For example, f(0) = 1 is considered an axiom. The goal is to define such statements and then prove simpler statements by randomly trying formulas until a solution is found.

Code Overview: Lexer, Parser, and Program

The C code includes the lexer, parser, and program components. The parse_program function uses parse_statement, which further uses parse_defines and parse_equality. The parse_equality function is responsible for parsing expressions involving an equal sign or an arrow. Currently, parse_equality contains a "to-do" item for implementation.

Implementing Parse Equality

The creator plans to implement parse_equality without operator precedence, parsing expressions from left to right. Parentheses will be used to define the order of operations. The function needs to handle different types of equalities, such as set definitions and expressions involving variables. The implementation will involve parsing expressions on both sides of the equal sign.

Parsing Expressions: Initial Token Analysis

The parse_expression function will determine the type of expression based on the initial token. It checks if the token is a number, set, or name. Numbers typically lead to operators, while names can indicate function calls or operators. Sets should be complete without additional elements. The function returns an error if the token doesn't match these expected types.

Handling Numbers in Expressions

If the token is a number, the next token must be an operator. The function checks the next token and sets the expression kind accordingly. If the next token is an equal sign, it's a number expression. If it's an operator, it's an operator expression. An error is thrown if neither is found. The function uses clitoral to create the number expression and reads the next token.

Creating Operator Expressions

For operator expressions, memory is allocated for the left and right hand sides. The left hand side is filled with the number, and the right hand side is parsed using parse_expression again. The function reads tokens to skip the number and the operator symbol before parsing the right hand side.

Testing the Implementation

The creator tests the implementation with an example: 1 + 1 = 2. The initial test reveals an error where the function expects an equal sign but finds a number. This is corrected by ensuring the function reads the current token without consuming it.

Handling Different Token Types

The function is modified to handle different token types, such as exists and for_all, which indicate the end of an expression. The first expression should end on an equal sign, while the second expression can end on various tokens. The function now correctly parses the example expression.

Dumping Expressions for Debugging

To better understand the parsed expressions, the creator adds a dump function to print the structure of the expressions. This involves creating functions to dump equalities, sets, numbers, functions, and operators. The dump function uses a switch statement to handle different expression kinds and prints the relevant information.

Parsing Names and Functions

The function is extended to handle names, which can be variables or function calls. If the next token is a left parenthesis, it's a function call; otherwise, it's a variable. The function initializes the expression kind and handles the arguments for function calls.

Handling Function Arguments

The creator considers allowing functions with only one argument and adds a "to-do" item to parse arguments. The function handles operators by allocating memory for the left and right hand sides and setting the token kind to function.

Parsing Parentheses

The function is updated to handle parentheses. If a left parenthesis is encountered, the function parses the expression inside the parentheses. The function reads the next token and recursively calls parse_expression to parse the inner expression.

Implementing Eval and Proof Statements

The creator adds support for eval and proof statements. The eval statement parses an expression, while the proof statement parses another statement. These are added to the parse_statement function to handle them correctly.

Final Adjustments and Testing

The code is adjusted to ensure that eval and proof statements are correctly parsed. The parse_expression function is modified to handle these statements. The implementation is tested to ensure it correctly evaluates expressions and proves statements.

Conclusion and Next Steps

The creator concludes that the parser is in a good state and expresses satisfaction with the progress. The next steps involve interpreting the abstract syntax tree (AST) and implementing type checking. The goal is to get the evaluation working and add a list of evaluations and proofs to the program. The creator also mentions potential command-line arguments using arc_parse.