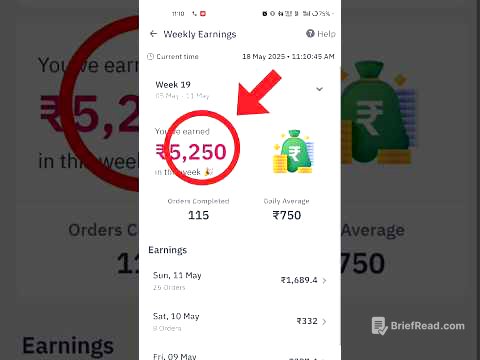
Okay, I'm ready to create a detailed summary of the YouTube video, focusing on clarity, accuracy, and a logical flow. I will use the provided transcript and timestamps to create chapter summaries, ensuring that key details and facts are retained.
TLDR;
This video by محمد أبو شاكر لعبودي للتعليم المتوسط provides a comprehensive explanation of how to solve a system of two equations with two unknowns using the substitution method. It covers identifying the easiest variable to isolate, performing the substitution, solving the resulting equation, and finding the values of both variables. The video uses a step-by-step approach with clear examples to guide students through the process.
- Explanation of the substitution method for solving systems of equations.
- Step-by-step guidance on isolating variables and performing substitutions.
- Practical examples to illustrate the method.
- Focus on accuracy and checking solutions.
Introduction to Solving Systems of Equations [0:00]
The video introduces the concept of solving a system of two equations with two unknowns. It highlights that the goal is to find the values of the variables (typically x and y) that satisfy both equations simultaneously. The presenter sets the stage for explaining the substitution method as a technique to achieve this.
Choosing the Variable to Isolate [0:28]
The presenter explains the initial step in the substitution method: identifying the easiest variable to isolate in either of the two equations. The aim is to choose the variable that requires the fewest algebraic manipulations to express it in terms of the other variable. This choice simplifies the subsequent steps and reduces the chances of errors.
Isolating the Variable [0:54]
Here, the presenter demonstrates the process of isolating the chosen variable. This involves performing algebraic operations (addition, subtraction, multiplication, or division) on both sides of the equation to get the selected variable alone on one side. The result is an expression that defines the variable in terms of the other variable.
Performing the Substitution [0:01]
With one variable isolated, the next step is to substitute the expression obtained into the other equation. This replaces the isolated variable in the second equation, resulting in a new equation that contains only one variable. This substitution is a crucial step in reducing the system to a single equation that can be solved directly.
Solving the Resulting Equation [0:01]
After the substitution, the presenter focuses on solving the single-variable equation. This involves using algebraic techniques to isolate the remaining variable and find its value. The presenter guides viewers through the necessary steps, such as combining like terms and performing inverse operations, to arrive at the solution for this variable.
Finding the Value of the Other Variable [0:02]
Once the value of one variable is found, the presenter explains how to determine the value of the other variable. This is done by substituting the known value back into the expression obtained when isolating the first variable. This calculation yields the value of the second variable, completing the solution of the system of equations.
Example 1: Solving the System [0:02]
The presenter provides a concrete example of solving a system of equations using the substitution method. The system is:
- x + y = 13
- x - y = 7
The presenter isolates x in the first equation (x = 13 - y) and substitutes it into the second equation. This leads to solving for y, and subsequently finding x.
Example 2: Solving the System [0:05]
A second example is presented with the following system:
- 2x + y = 1
- x - 2y = -3
The presenter isolates x in the second equation (x = 2y - 3) and substitutes it into the first equation. This results in an equation with only y, which is then solved. The value of y is then used to find the value of x.
Checking the Solution [0:08]
The presenter emphasises the importance of verifying the solution by substituting the values of x and y back into the original equations. If both equations are satisfied, the solution is correct. This step helps to catch any errors made during the solving process and ensures the accuracy of the answer.